算数

　　　　
　　　　「立体の図形の体積」

　　　　立体の体積を考える問題は、いろいろな事がらと組み合わされて問われます。この問題でも相
　　　　似の考え方を用いて解くことが必要です。

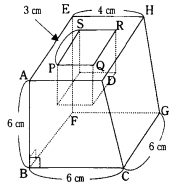
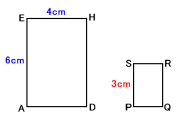
＜問題＞ 下の図のような底面ＡＢＣＤが台形の形をした四角柱があります。この四角柱の体積が になるように直方体の穴を掘ります。穴の表面ＰＱＲＳはこの四角柱の表面ＡＤＨＥ と同じ形です。穴のたて(ＰＳ)の長さが３cmのとき、次の問いに答えなさい。 (1) 穴のよこ(ＳＲ)の長さは何cmですか。 (2) 穴の深さは何cmですか。 ＜解答＞ (1) 四角形ＰＱＲＳと四角形ＡＤＨＥが相似です。 　　相似比は、ＰＳ：ＡＥ＝６：３＝２：１ 　　これより、 　　　ＳＲ＝ＥＨ×＝２cm 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　２cm (2) 穴がない場合の四角柱ＡＢＣＤ−ＥＦＧＨの体積は、 　　　底面積＝(４＋６)×６×＝３０ｃm3 　　　高さ＝６cm 　　を使って、 　　　３０×６＝１８０ｃm3 　　穴を掘ると体積がになるので、 　　穴の体積は、四角柱ＡＢＣＤ−ＥＦＧＨの体積の体積の(１−＝）です。 　　　穴の体積＝１８０×＝３０ｃm3 　　穴は直方体なので、 　　　ＰＳ×ＳＲ×深さ＝３０ 　　　深さ＝３０÷３÷２＝５cm 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　５cm

ページTopへ