＜問題＞
太郎君はＢ地からＡ地に向かって歩きました。花子さんは太郎君と同時にＡ地を出発し
て自転車でＢ地に向かいました。次のグラフは２人の進んだようすを表したものです。
次の問いに答えなさい。
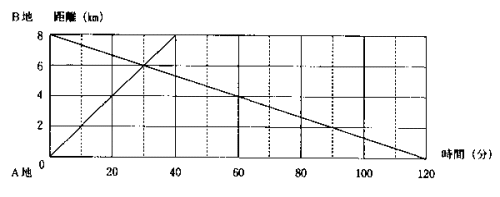
(1) 太郎君は出発してから何分後に花子さんと会いましたか。また、その場所はＢ地から
何kmのところですか。
(2) 花子さんはＢ地で１０分間休んだ後、Ｂ地に向かった速さと同じ速さでＡ地に帰りま
した。花子さんがＢ地に着いてからＡ地に帰るまでのようすをグラフに書き入れなさい。
(3) 花子さんが帰りに太郎君に追いつくのは、Ａ地から何kmのところですか。
＜解答＞
(1) グラフを読むと、出発して３０分後、Ａ地から６kmのところですれ違っていることが
わかります。
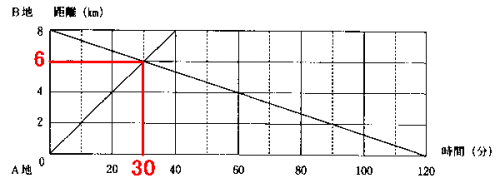
Ａ地から６kmの地点は、Ｂ地から(８−６＝)２kmの地点です。
答 ３０分後、Ｂ地から２kmの場所
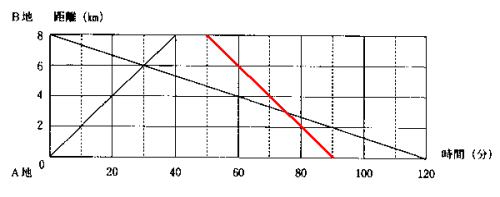
(2) 花子さんがＢ地を出たのは、Ａ地を出てから(４０＋１０＝)５０分後です。
また、Ｂ地からＡ地までにかかる時間は、Ａ地からＢ地までにかかる時間と同じです。
よって、Ａ地に戻ってくるのは、Ａ地を出てから（５０＋４０＝）９０分後です。
これをもとにグラフを書くと次のようになります。
(3) よく使う考え方が２つあります。
<1> 旅人算の考え方を用いる場合
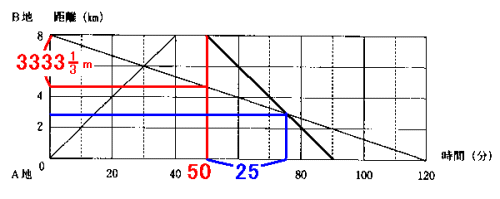
太郎君の速さは、Ｂ地からＡ地までの８kmに１２０分かかっているので、
８０００ｍ÷１２０分＝毎分６６
ｍ 花子さんの速さは、同じ距離に４０分かかっているので、
８０００ｍ÷４０分＝毎分２００ｍ
花子さんがＢ地を出た時、太郎君がＢ地から進んだ距離は、
毎分６６
ｍ×５０分＝３３３３
ｍ花子さんが太郎君に追いつくまでにかかる時間は、
３３３３
ｍ÷(毎分２００ｍ−毎分６６ｍ）＝２５分太郎君に追いつくのは、Ａ地に戻るまであと(４０−２５＝)１５分の地点です。
毎分２００ｍ×１５分＝３０００ｍ＝３km
<2> 速さの比を用いて考える場合
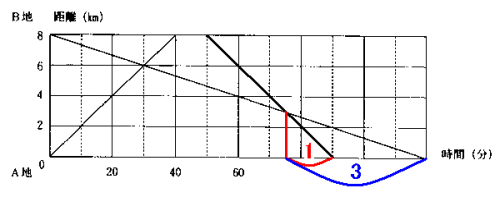
２人の速さの比は、 太郎君：花子さん＝毎分６６
ｍ：毎分２００ｍ＝１：３花子さんが太郎君に追いついた地点からＡ地までにかかる時間の比を考えると、
太郎君：花子さん＝１：
＝３：１この時間差が(１２０−９０＝)３０分なので、
花子さんが太郎君に追いついた地点からＡ地までにかかる時間は、
３０分×
＝１５分これより、
毎分２００ｍ×１５分＝３０００ｍ＝３km
＊グラフが書かれているので、<２>の考え方で解けると時間がかかりません。