算数

　　　　「相似な三角形の辺の長さと面積」

　　　　このタイプの問題は中学入試で最も出題の多いもののひとつです。いろいろな
　　　　図形の組み合わせで出題されています。
　　　　以下の問題は最もオーソドックスな「平行線で三角形を分ける問題」なので、
　　　　練習問題に使っても良いものです。

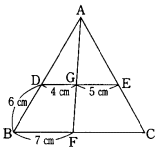
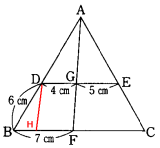
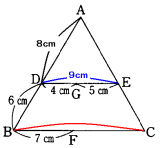
＜問題＞ 　次の図においてＤＥとＢＣが平行であるとき、次の問に答えなさい。 (1) ＡＤの長さを求めなさい。 (2) ＢＣの長さを求めなさい。 (3) 三角形ＡＤＧと台形ＧＦＣＥの面積を最も簡単な比で表しなさい。 ＜解答＞ (1) ２つの三角形ＡＢＦとＡＤＧの相似を利用するのがテキストなどでは一般的ですが、 　　以下の考え方の方がミスなくできます。 　　次のように、点Ｄから線分ＡＦに平行な線分ＤＨを引きます。 　　２つの三角形ＤＢＨとＡＤＧが相似で、その相似比は、 　　　ＢＨ：ＤＧ＝(７−４)：４＝３：４ 　　これより、 　　　ＡＤ＝ＤＢ×＝６cm×＝８cm 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　８cm (2) ２つの三角形ＡＢＣとＡＤＥが相似です。 　　その相似比は、 　　　ＡＢ：ＡＤ＝(８＋６)：８＝７：４ 　　これより、 　　　ＢＣ＝ＤＥ×＝(４＋５)×＝１５cm 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１５cm (3) ２つの三角形ＡＤＧとＡＧＥは高さが等しいので、面積比は底辺の比と同じです。 　　　ＤＧ：ＧＥ＝４：５ 　　２つの三角形ＡＦＣとＡＧＥは相似なので、面積比は相似比(７：４)の２乗の比です。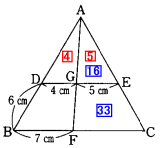 　　　(７×７)：(４×４)＝４９：１６ 　　これより、三角形ＡＧＥと台形ＧＦＣＥの面積比は、 　　　１６：(４９−１６)＝１６：３３ 　　次のように連比を作って、 　　　三角形ＡＤＧ：三角形ＡＧＥ：台形ＧＦＣＥ 　　　　　　４　　：　　　５ 　　　　　　　　　　　　１６　　：　　３３ 　　　　 　　　　　６４　　：　　８０　　：　１６５ 　　三角形ＡＤＧと台形ＧＦＣＥの面積比は、 　　　６４：１６５ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　６４：１６５

ページTopへ