<問題>
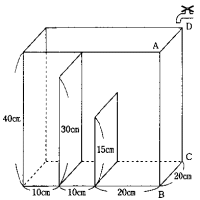
次図のような直方体の水そうがあります。この水そうの面ABCDに平行に2つのしき
りをつけました。(しきりの厚さは考えないものとします。)この水そうに図の位置にある
給水口から水を毎秒100cm3の割合で入れたとき、次の問いに答えなさい。
(1) 満水になるまでの時間は何分何秒ですか。
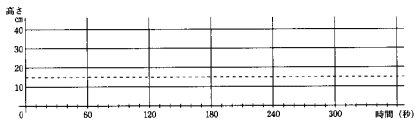
(2) 満水になるまでの間の、ABで測った水面の高さと時間の関係のグラフをかきなさい。
<解答>
(1) 直方体の容器の容積は、
20×(10+10+20)×40=32000cm3
毎秒100cm3の割合で水を入れるので、満水になるまでの時間は、
32000÷100=320秒=5分20秒
答 5分20秒
(2) 仕切りがあるために水の深さが変わらない時間帯があるため、折れ線グラフとなりま
す。その境目となる時間と深さを考えていきます。
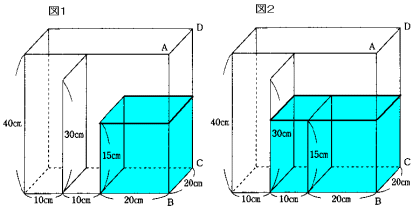
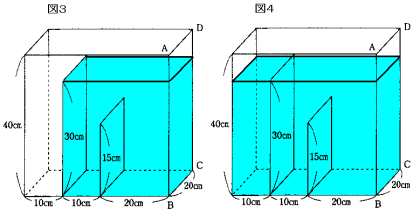
図1の状態になるまでは一定の割合で深さが増していきます。
図1の時の水の深さは、 15cm
図1の時の水の体積は、 20×20×15=6000cm3
図1になるまでの時間は、6000÷100=60秒
図1から図2の状態になるまでは深さは変わりません。
図2の時の水の深さは、 15cm
図2の時の水の体積は、 20×(10+20)×15=9000cm3
図2になるまでの時間は、9000÷100=90秒
図2から図3の状態になるまでは一定の割合で深さが増していきます。
図3の時の水の深さは、 30cm
図3の時の水の体積は、 20×(10+20)×30=18000cm3
図3になるまでの時間は、18000÷100=180秒
図3から図4の状態になるまでは一定の割合で深さが増していきます。
図4の時の水の深さは、 30cm
図4の時の水の体積は、 20×(10+10+20)×30=24000cm3
図4になるまでの時間は、24000÷100=240秒
以下満水なるまで一定の割合で深さが増していきます。
満水の時の水の深さは、 40cm
満水になるまでの時間は、320秒
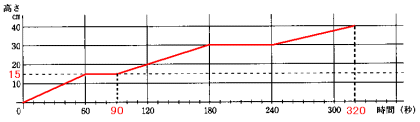
これらの数値をもとにグラフを書くと、次のようになります。