＜問題＞
次の図のように、辺ＡＤと辺ＢＣが平行な台形ＡＢＣＤがあります。点Ｐは辺ＢＣ上を
ＢからＣまで秒速１cmで進みます。次の問いに答えなさい。
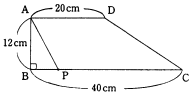
(1) 点ＰがＢを出発してから５秒後の三角形ＡＢＰの面積は何ｃm2ですか。
(2) 四角形ＡＰＣＤが平行四辺形になるのは、点ＰがＢを出発してから何秒後ですか。
(3) 三角形ＡＢＰの面積が、四角形ＡＰＣＤの面積の
になるのは、点ＰがＢを出発してから何秒後ですか。
＜解答＞
(1) ５秒後の直角三角形ＡＢＰは次の図のようになります。
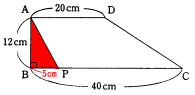
辺ＢＰの長さ 秒速１cm×５秒＝５cm
三角形ＡＢＰの面積 ５×１２÷２＝３０ｃm2
答 ３０ｃm2
(2) １組の向い合う辺が平行で長さが等しいときに平行四辺形になります。
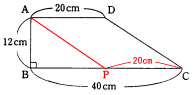
この問題の場合に条件を満たすのは、
辺ＰＣの長さ＝辺ＡＤの長さ＝２０cm
よって、
点Ｐの進んだ距離＝４０−２０＝２０cm
その時までの時間＝２０cm÷秒速１cm＝２０秒
答 ２０秒後
(3) 高さの等しい三角形の面積比は底辺の長さの比になるので、
台形は高さの等しい２つの三角形に分けて考えます。
与えられた割合
を比に直すと、三角形ＡＢＰの面積：台形ＡＰＣＤの面積＝１：４
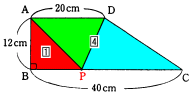
この結果から、
ＢＰの長さ：(ＰＣの長さ＋ＡＰの長さ)＝１：４
また、
ＢＰの長さ＋ＰＣの長さ＋ＡＰの長さ＝４０＋２０＝６０cm
よって、
ＢＰの長さ＝６０×
＝１２cm点Ｐの進んだ距離が１２cmなので、その時までの時間は、
１２cm÷秒速１cm＝１２秒
答 １２秒