＜問題＞
次の各問いに答えなさい。
(1) 高さが５ｍの街灯から３ｍ離れた地点に２ｍの棒が垂直に立てられています。
このとき、棒の影の長さを求めなさい。
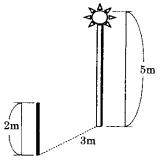
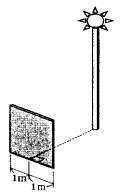
(2) ２ｍの棒のかわりに１辺が２ｍの正方形の看板が立てられています。
このとき、影の面積を求めなさい。
＜解答＞
(1) 影の問題は適切な三角形をの相似を考えると解くことができます。
次の図のように真横から見た図を考えるます。□ｍが影の長さにあたります。
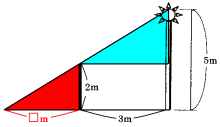
赤い三角形と水色の青い三角形は相似なので、
□：２＝３：(５−２）
□＝２×３÷(５−２)＝２ｍ
答 ２ｍ
(2) 次の図のような三角錐を考えて、台形ＢＥＦＣの面積を求めます。
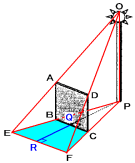
三角形ＯＥＰと三角形ＡＥＢが相似で、
その相似比は、
ＯＰ：ＡＢで求めて、５：２
よって、
ＯＥ：ＡＥ＝５：２…(a)
また、三角形ＯＡＤと三角形ＯＥＦも相似で、
その相似比は、(a) を利用して
ＯＡ：ＯＥ＝(ＯＥ−ＡＥ)：ＯＥ＝３：５
よって、
ＡＤ：ＥＦ＝３：５
ＥＦ＝ＡＤ×５÷３＝３
ｍまた、高さＱＲは(1) で求めた影の長さと同じです。
台形ＢＥＦＣの面積＝(ＢＣ＋ＥＦ)×ＱＲ÷２
＝(２＋３
)×２÷２＝５
ｃm2答 ５
ｃm2＊他にもいくつか計算法がありますが、いずれも相似を利用してＥＦの長さを求める必
要があります。