<問題>
1目もり1cmの方眼紙の上に、図1のような図形をかき、切りぬきました。
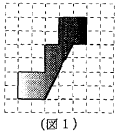
同じ図形をたくさん用意します。これらの図形を図2から図6のように並べ、模様を作
ります。
この模様の左の端から右の端までの横の長さを、図に示されているように、模様の長さ
とします。
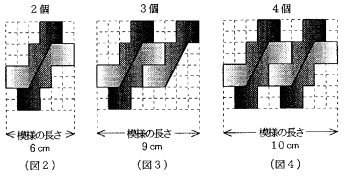
(1) 次の( )にあてはまる数を入れなさい。
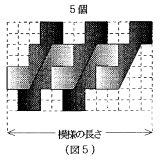
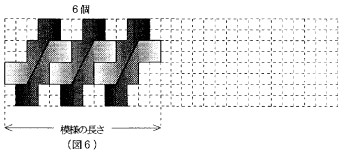
模様の長さは、図形を5個並べたとき( )cm、6個並べたとき( )cmです。
7個並べると( )cmになります。
(2) 図形を15個並べると、模様の長さは何cmになりますか。
(3) 図形を何個並べると、模様の長さが62cmになりますか。
<解答>
(1) 図から1個めを除く奇数個めを並べるとは3cm、偶数個めを並べると1cm、それぞれ
前の長さより長くなるのことがわかります。
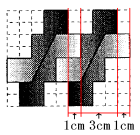
5個並べたときの長さ=4個並べたときの長さ+3cm
=10cm+3cm
=13cm
6個並べたときの長さ=5個並べたときの長さ+1cm
=13cm+1cm
=14cm
7個並べたときの長さ=6個並べたときの長さ+3cm
=14cm+3cm
=17cm
答 13、14、17
(2) 1〜15にある奇数と偶数の個数を数えます。
1を除く奇数の個数は、(15−1)÷2=7個
偶数の個数は、 (14−2)÷2+1=7個
これより、
15個並べたときの長さ=5cm+3cm×7+1cm×7
=33cm
答 33cm
(3) 2個目以降で増えた長さは、
62cm−5cm=57cm
伸びる長さは 1cm、3cm の繰り返しです。これを1組として考えると、
57cm÷(1cm+3cm)=14組あまり1cm
全部の個数は、
1+2×14+1=30個
答 30個