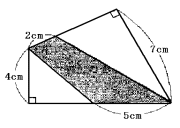
<問題> 下の図での影の部分の面積を求めなさい。
(1)
(2)
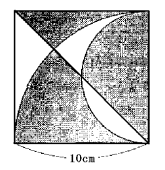
<解答>
(1) 直角に交わる辺に目をつけて、底辺と高さの組が分かる2つの三角形に分けます。
四角形AFCDを2つの三角形AECとAFCに分けことができます。
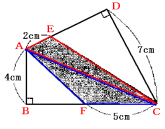
三角形AECは底辺がAEで高さがCDとなります。
三角形AECの面積=2×7÷2
=7cm2
三角形AFCは底辺がAFで高さがABになります。
三角形AFCの面積=5×4÷2
=10cm2
四角形AFCDの面積は、
7+10=17cm2
答 17cm2
(2) 合同な部分を動かして形を計算しやすく変えます。
左図の赤い部分と青い部分を矢印の場所に移動させると、右図の図形ができます。
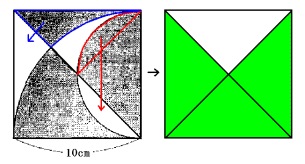
影の部分の面積は正方形を4等分したうちの3個分にあたるので、
10×10÷4×3=75cm2
答 75cm2