<問題>
次の図のように1段目に1個、2段目に3個、3段目に5個、……となるように自然数
を順に並べました。このとき、次の問いに答えなさい。
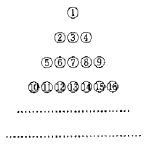
(1) 上から10段目の1番左の数はいくつですか。
(2) 230は上から何段目で左から何番目ですか。
(3) 1から下へ各段の真ん中の数を順に見ていきます。たとえば、2段目は3で、3段目
は7です。100段目の数が9901のとき、101段目の数はいくつですか。
<解答>
(1) 各段の1番右の数を見るとすべて平方数になっています。
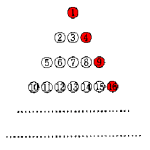
1段目 1×1= 1
2段目 2×2= 4
3段目 3×3= 9
4段目 4×4=16
10段目の1番左の数は9段目の1番右の数に1を加えたものなので、
9×9+1=82
答 82
(2) 10段目から下の段で各段の1番右の数を考えます。
10段目 10×10=100
11段目 11×11=121
12段目 12×12=144
13段目 13×13=169
14段目 14×14=196
15段目 15×15=225
16段目 16×16=256
230は226以上256以下の範囲に入るので上から16段目の数です。
上から16段目の数を左から順に書いていくと、
226、227、228、229、230、…
よって、230は上から16段目で左から5番目の数だとわかります。
答 上から16段目で左から5番目
(3) 「101段めの真ん中の数は何か」という問いになるのが一般的なので、2つの解法
を示します。

解法1)9901を使わないで解きます。
等差数列では「真ん中の数=両端の数の和÷2」が成り立つことを利用して、
101段目の1番左の数 100×100+1=10001
101段目の1番右の数 101×101=10201
101段目の真ん中の数 (10001+10201)÷2=10101
解法2)問題に即して9901を使って解きます。
各段の真ん中の数どうしで差を考えると、
2段目と1段目の差 3−1=2=1×2
3段目と2段目の差 7−3=4=2×2
4段目と3段目の差 13−7=6=3×2
差はいつも上の段の数の2倍だとわかります。
101段目の真ん中の数 9901+(101−1)×2=10101
答 10101