＜問題＞

　次の図のような正方形ＡＢＣＤと、ＥＦとＥＧの長さが等しい二等辺三角形ＥＦＧがあ
ります。二等辺三角形ＥＦＧが図の位置から毎秒２ｃｍの速さで、矢印の方向に直線ｍに
沿ってＧがＢと重なるまで移動するものとします。次の問いに答えなさい。




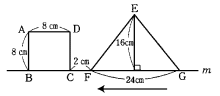
(1) ２つの図形の重なった部分が正方形であるのは、何秒間ですか。


(2) ７秒後の重なった部分の図形は何角形ですか。


(3) ２つの図形の重なった部分が台形になるのは２回あります。 何秒後から再び台形に
　なりますか。














＜解答＞

(1) 正方形ＡＢＣＤが二等辺三角形ＥＦＧと完全に重なっている時間です。正方形の上の
　　辺ＡＤが二等辺三角形ＥＦＧと重なる時間を考えます。

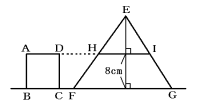
　　上の図のように辺ＡＤと重なる部分ＨＩの長さは、三角形の相似を利用して、

　　ＨＩ：ＦＧ＝１６ｃｍ：（１６ｃｍ−８ｃｍ）
　　　　　　　＝２：１

　　ＨＩ＝２４ｃｍ×１÷２
　　　　＝１２ｃｍ




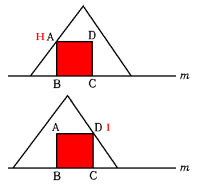
　　点Ｈが頂点Ａがと重なってから点Ｉが点Ｄと重なるまでが正方形になります。

　　二等辺三角形ＥＦＧが進んだ距離　　１２ｃｍ−８ｃｍ＝４ｃｍ

　　その間にかかった時間　　　　　　　４ｃｍ÷毎秒２ｃｍ＝２秒

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　２秒



(2) 三角形の相似を利用して７秒後の図を描いて考えます。

　　二等辺三角形ＥＦＧが進んだ距離は、

　　毎秒２ｃｍ×７秒＝１４ｃｍ
　　　
　　点Ｆの位置は頂点Ｂから左へ

　　１４ｃｍ−（２ｃｍ＋８ｃｍ）＝４ｃｍ

　　これをもとに７秒後の図を描きます。




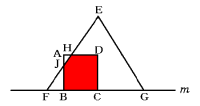
　　この図を見ると五角形だとわかります。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　五角形



(3) 頂点Ｇが頂点Ｃと重なるとそれまでの五角形から台形に変わります。



　　（２４ｃｍ＋２ｃｍ）÷毎秒２ｃｍ＝１３秒

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１３秒後