次の(図2)は三角柱と円柱の半分を組み合わせた立体(図1)を、正面とま上から見
た図です。
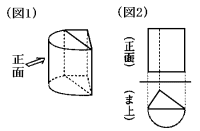
これを参考にして、(図3)について、(1)、(2)、(3) の問いに答えなさい。
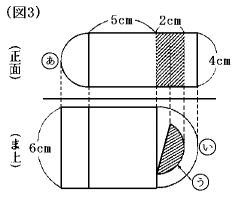
(図3)は、いくつかの立体を組み合わせたある立体から、斜線部分でできる立体をく
りぬいた立体を、正面とま上から見た図です。
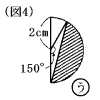
曲線部分あといは円の半分で、曲線部分うは半径2cm、2本の半径の作る角が150
度の円の一部分((図4)を参考にしなさい)です。
円周率は3.14とし、答えは小数第2位を四捨五入して、小数第1位まで求めなさい。
(1) 斜線部分でできる立体をくりぬく前の立体の展開図の面積を求めなさい。
(2) ま上から見た図の斜線部分の面積を求めなさい。
(3) 斜線部分をくりぬいた後に残った立体の体積を求めなさい。
<解答>
(1) くり貫く前の立体の展開図は次のような2つの図形の組み合わせです。
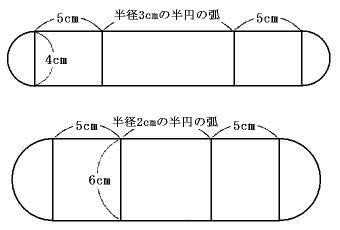
上の図は正面、その裏側、右側の曲面を組み合わせて1枚の図形にしたものです。
長方形と円の面積の和と考えて、
4×(5+6×3.14×+5)+2×2×3.14
=4×10+3.14×(12+4)
=40+50.24
=90.24cm2
下の図は真上、その裏側、左側の曲面を組み合わせて1枚の図形にしたものです。
同様に考えて、
6×(5+4×3.14×+5)+3×3×3.14
=6×10+3.14×(12+9)
=60+65.94
=125.94cm2
立体の表面積は、
90.24+125.94=216.18cm2
小数第2位で四捨五入して、答は 216.2cm2 です。
答 216.2cm2
*3.14をどの段階でかけるかによって式が異なります。上の式はその1例です。
(2) 下の図で赤い直角三角形の3つの角は30度、60度、90度です。
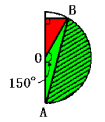
このような直角三角形は正三角形を対称軸で2等分したもので、最も短い辺と最も長
い辺の長さの比は 1:2 です。
この関係を利用すると三角形OABの高さがおうぎ形の半径のだとわかります。
斜線部の面積はおうぎ形OABの面積と三角形OABの面積の差なので、
2×2×3.14×−2×(2×)×
=5.23…−1
=4.23…cm2
小数第2位で四捨五入して、答は 4.2cm2 です。
答 4.2cm2
(3) くり貫く前の立体は半円柱2つと直方体1つの複合立体です。それからくり貫いた部
分を除いて計算します。
2つの半円柱は、
1.底面の半径2cm、高さ6cm
2.底面の半径3cm、高さ4cmも
直方体は、
縦6cm、横5cm、高さ4cm
くり貫く部分(柱体)は、
底面積4.2cm2、高さ4cm
これらの値を使って、
2×2×3.14××6+3×3×3.14××4+6×5×4−4.2×4
=3.14×(12+18)+120−16.8
=94.2+120−16.8
=197.4cm2
*上は設問の順序から考えて、くり貫く立体の底面積を4.2cm2を底面積として計
算しています。これを分数を用いて表して計算後に小数に直すと、計算結果が異な
ります。その場合、答は 197.3cm2 です。
大学入試などでは、四捨五入の場所によって生じる値のちがいはかなりの範囲で許
されます。
答 197.4cm2 または 197.3cm2