＜問題＞　

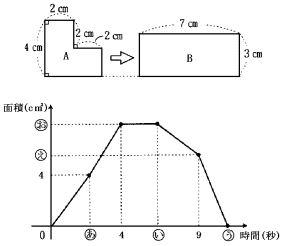
　下の図のような図形Ａと長方形Ｂがあります。図形Ａは矢印の方向に毎秒ｌcmで動き、
長方形Ｂ上を通過します。下のグラフは、図形Ａが長方形Ｂに重なり始めてから終わるま
での時間と、重なった部分の面積の関係を表しています。このとき、次の問いに答えなさ
い。

(1) グラフ上の　あ　〜　お　はそれぞれいくつですか。


(2) 重なった部分の面積が７ｃm2になるのは重なり始めてから何秒後ですか。(計算・や
　り方を書きなさい)



















＜解答＞

(1) あ秒後、４秒後、い秒後、９秒後、う秒後の各時点の状態を図に表して考えます。

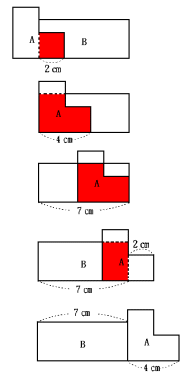
　　　あ：２ｃｍ÷毎秒１ｃｍ＝２秒

　　　い：７ｃｍ÷毎秒１ｃｍ＝７秒

　　　う：（７ｃｍ＋４ｃｍ）÷毎秒１ｃｍ＝１１秒

　　　え：９秒後の面積
　　　　　　３ｃｍ×２ｃｍ＝６ｃm2

　　　お：４秒後の面積
　　　　　　３ｃｍ×４ｃｍ−１ｃｍ×２ｃｍ＝１０ｃm2

　　　　　　　　　　　　　　　　　答　あ：１　い：７　う：１１　え：６　お：１０

(2) あてはまる時点がグラフでどの線分上にあるかを考えて解きます。

　　次の図のように重なった部分の面積が７ｃm2になるのは２度あります。



　　１度目は２秒後から４秒後の間、２度目は７秒後から９秒後の間です。

　　ａ）１度目

　　　　２秒後から４秒後の間で面積が増える割合は、

　　　　　（１０ｃm2−４ｃm2）÷（４秒−２秒）＝毎秒３ｃm2

　　　　よって７ｃm2になるのは、

　　　　　２秒＋（７ｃm2−４ｃm2）÷毎秒３ｃm2＝３秒後

　　ｂ）２度目

　　　　７秒後から９秒後の間で面積が減る割合は、

　　　　　（１０ｃm2−６ｃm2）÷（９秒−７秒）＝毎秒２ｃm2

　　　　よって７ｃm2になるのは、

　　　　　７秒＋（１０ｃm2−７ｃm2）÷毎秒２ｃm2＝８秒後

　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３秒後と８秒後