次の図のような長方形ABCDがあります。いま、点Pが図のように点Bから動きはじ
め、辺ADと点Eではねかえり、図のように長方形ABCDの4つの辺にはねかえりなが
ら動きます。このとき、あとの問いに答えなさい。
ただし、BE=3cmとします。
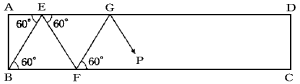
(1) 点Pが点Bを出発してからBCと3回目にはねかえる点Qとします。
点Qではねかえった直後にCDとはねかえる点Rととします。
RQ=2cmのとき、BCの長さは何cmか求めなさい。
(2) 点Pが点Bを出発してからちょうど点Cにきたときに止まりました。
BC=20cmのとき、点Pが動いた距離を求めなさい。
<解答>
(1) 次の図のように点Pは動きます。
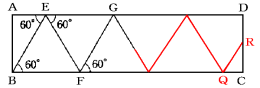
正三角形を描きながら進んでいくので、
BQ=BE×3=9cm
最後にできる直角三角形QRCは、三角定規の細長い方と相似で最長の辺と最短の辺
との長さの比が2:1です。
BQ=RQ×
よって、
BC=BQ+BQ=10cm
答 10cm
(2) 下の図のように辺(青線)で反射する時に、その辺を対象の軸として長方形を描くと、
点Pの動きは折り返さずにそのまま伸ばして考えることができます。
(注:図の点Pの進み方は参考図として示したもので問題とは一致しません)
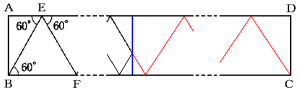
点Pが点Cで止まるということは何個かの正三角形が並んで半端の部分はできない場
合です。
このとき長方形の横の長さは20と3の最小公倍数で60cmです。
BFの間で考えると、点Pは正三角形の2辺にあたる折れ線(BE+EF)を動くこ
とがわかります。これが何度か繰り返されるので、点Pの動いた距離は長方形の横の
長さの2倍と等しくなります。
60×2=120cm
答 120cm