＜問題＞
　次の図のような、１辺の長さが１cmの正方形の対角線の長さを１ルートルと呼ぶことに
します。１ルートルが１目盛りになっている定規があります。

　　　

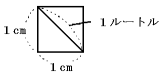
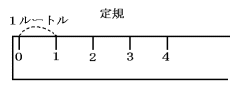
　次の［　ア　］から［　エ　］にあてはまる数を求めない。

(1) この定規で、１辺の長さが１ルートルの正方形を書きました。この正方形形の面積は
　［　ア　］ｃm2です。


(2) １辺の長さが３ルートルの正方形の面積は［　イ　］ｃm2なので、この正万形の中に
　１辺の長さが１cmの正方形の板を同じ向きに並べると、最大［　ウ　］枚まで並べるこ
　とができます。


(3) たて３ルートル、横５ルートルの長方形の中に、１辺の長さが１cmの正方形の板を同
　じ向きに並べると、最大［　エ　］枚まで並べることができます。
















＜解答＞

(1) 次の図のように対角線の長さが２cmの正方形（赤）ができます。



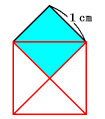
　　　２×２÷２＝２ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　ア＝２


(2) 上を参考に考えると、１辺が３ルートルの正方形は対角線が６cmあることがわかりま
　　す。（相似形の面積比と線分の長さの比を使って考えても良いでしょう）

　　この正方形の面積は、

　　　６×６÷２＝１８ｃm2

　　(1) の結果から１辺１ルートルの正方形の面積が２ｃm2なので、

　　　１．４×１．４＝１．９６
　　　１．５×１．５＝２．２５

　　の計算から、１ルートルは１．４cmより長く１．５cmより短いことがわかります。

　　　１．４×３＝４．２
　　　１．５×３＝４．５　　
　　　
　　３ルートルは４．２cmより長く４．５cmより短いので、次の図のように正方形が１６
　　個入ります。



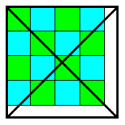
　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　イ＝１８、ウ＝１６


(3) ５ルートルは７cmより長く７．５cmより短い長さです。

　　縦に４枚、横に７枚並べることができるので、

　　　４×７＝２８枚

　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　エ＝２８