図のように、半径2cmの円が、縦20cm、横18cmの長方形の内側を辺に沿ってころが
っています。円はア→イ→ウ→エ→ア→……の順にころがるものとします。
このとき、次の各問いに答えさない。
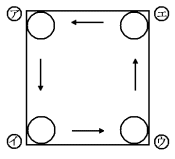
(1) 円の中心が移動した距離が46cmのとき、円はア、イ、ウ、エのどこにありますか。
また、円の通過した部分の面積を求めなさい。
(2) 円の中心が移動した距離が56cmのとき、円の通過した部分の面積を求めなさい。
<解答>
(1) 中心の移動を図に表して考えます。中心の移動距離は長方形の辺よりも半径2つ分だ
け短くなります。
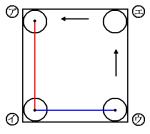
縦方向へ転がるときの中心が移動する距離(赤線)は、
20−2×2=16cm
横方向へ転がるときの中心が移動する距離(青線)は、
18−2×2=14cm
46cm=16cm+14cm+16cmなので、エに達しています。
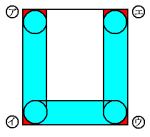
図の青い部分が円が通った部分です。全体の長方形から真ん中の白い長方形と赤い図形
6つを除いて求めます。
全体の長方形の面積 20×18=360cm2
白い長方形の面積 (20−2×2)×(18−2×2×2)=160cm2
赤い図形を4つ集めると1辺4cmの正方形から半径2cmの円を除いた部分になります。

赤い図形6つの面積の和 (4×4−2×2×3.14)÷4×6=5.16cm2
求める部分の面積は、
360−(160+5.16)=194.84cm2
答 エ、194.84cm2
(2) 56cm=14cm+14cm+16cm+10cmなので、中心がエの左へ10cmの位置に
あります。あと4cmでアの位置に戻るので、下の図のようになります。
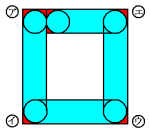
青い部分が円が通った部分です。全体から真ん中の白い長方形と赤い図形を7つ除いて
求めることができます。
全体の長方形の面積 20×18=360cm2
白い長方形の面積 (20−2×2×2)×(18−2×2×2)=120cm2
赤い図形を4つ集めると1辺4cmの正方形から半径2cmの円を除いた部分になります。
赤い図形7つの面積の和 (4×4−2×2×3.14)÷4×7=6.02cm2
求める図形の面積は、
360cm2−(120cm2+6.02cm2)= 233.98cm2
答 233.98cm2