＜問題＞

　次の図のような３つの辺の長さが３cm、４cm、５cmの直角三角形を６つ並べます。次の
問いに答えなさい。ただし、答えは小数第１位を四捨五入しなさい。

　　　　


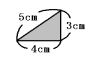
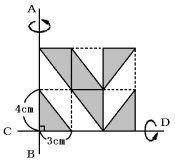
(1) この図形をＡＢのまわりに回転したときにできる立体の体積を求めなさい。なお、求
　め方も説明しなさい。


(2) この図形をＣＤのまわりに回転したときにできる立体の体積を求めなさい。















＜解答＞

(1) 回転軸から等しい距離にある点はすべて等しい長さの弧を描きます。このことをもと
　　に考えると、回転軸から等しい距離にある合同な図形によってできる回転体の体積は
　　等しくなると考えられます。

　　次の図のようにもとの図形を変形してもできる回転体の体積は変わりません。




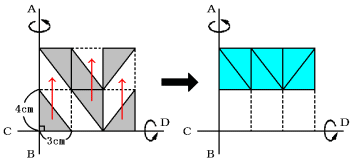
　　できる立体は円柱になります。

　　底面の半径は（３×３＝）９cm、高さは４cmなので、
　
　　　９×９×３．１４×４＝１０１７．３６ｃm3

　　小数第１位を四捨五入して、

　　　１０１７ｃm3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１０１７ｃm3


(2) 同様に考えます。いろいろな求め方がありますが、ここでは回転軸を底面とする平行
　　四辺形と三角形を作って考えます。




　　
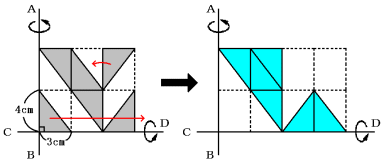
　　新しくできた図形の左側の部分の回転体は円柱から円錐を除いた立体です。

　　　８×８×３．１４×６−８×８×３．１４×６÷３
　　　＝８×８×３．１４×４
　　　＝３．１４×２５６

　　右側の図形の回転体は円錐を２つ組み合わせた立体です。

　　　（４×４×３．１４×３÷３）×２＝３２×３．１４

　　求める立体の体積は、

　　　３．１４×２５６＋３．１４×３２＝３．１４×２８８
　　　　　　　　　　　　　　　　　　　＝９０４．３２ｃm3

　　小数第１位を四捨五入して、

　　　９０４ｃm3


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　９０４ｃm3