立方体ABCD−EFGHがあります。辺AB、BC、CD、DAのまん中の点をそれ
ぞれP、Q、R、Sとします。このとき、次の問に答えなさい。
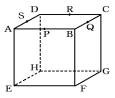
(1) 8つの点E、F、G、H、P、Q、R、Sのうちの2つの点を通る直線は全部で何本
ありますか。
(2) 8つの点E、F、G、H、P、Q、R、Sのうちの3つの点を頂点とする三角形のう
ち、二等辺三角形でないものは全部で何個ありますか。
<解答>
(1) どの3つの点も一直線上にありません。よって、8個から2個を選ぶ組み合わせとし
て求めることができます。
(8×7)÷(2×1)=28本
答 28本
(2) まず、8個から3個選ぶ組み合わせの計算を使って三角形の総数を求めます。
(8×7×6)÷(3×2×1)=56個
次に、二等辺三角形になるものを求めます。最初に底辺上にない1点を選んでから考
えると面対称の位置になる2点を結んで底辺を決めることができます。
ア)正方形EFGHの頂点で底辺上にない1点を選んだ場合
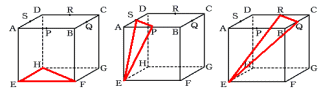
点Eを選ぶと、底辺はFH、PS、QRのいずれかに決まります。
点F、G、Hも同様になるので、
3個×4=12個
イ)正方形PQRSの頂点で底辺上にない1点を選んだ場合
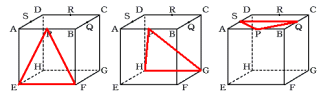
点Pを選ぶと、底辺はQS、EF、GHのいずれかに決まります。
点Q、R、Sも同様になるので、
3個×4=12個
よって、二等辺三角形でないものは、
56−(12+12)=32個
答 32個