＜問題＞

　図の四角すいＰ−ＡＢＣＤは底面が正方形で、その対角線の交点をＨとするとき、ＡＣ
＝ＢＤ＝ＰＨ＝８cmです。ＰＢの真ん中の点をＭ、ＰＤの真ん中の点をＮとし、この四角
すいを、３点Ａ、Ｍ、Ｎを通る平面で切ったとき、その平面とＰＣとの交点をＱとします。




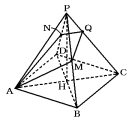
　このとき、次の問いに答えなさい。

(1) 四角すいＰ−ＡＢＣＤの体積を求めなさい。


(2) △ＰＡＱの面積を求めなさい。















＜解答＞

(1) この四角錐Ｐ−ＡＢＣＤは、

　　　底面積＝８×８×＝３２ｃm2

　　　高さ＝８cm

　　よって、

　　　体積＝３２×８×＝８５ｃm3


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　８５ｃm3


(2) 下図のように三角形ＰＡＢについて考え、三角形ＡＰＱが三角形ＡＣＰの何倍の
　　面積になるかを考えます。





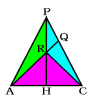
　　三角形ＡＰＲと三角形ＣＰＲとの面積比はＡＨ：ＣＨの比と同じです。

　　　三角形ＡＰＲ：三角形ＣＰＲ＝ＡＨ：ＣＨ＝１：１

　　三角形ＡＣＲと三角形ＡＣＰとの面積比はＲＨ：ＰＨの比と同じです。

　　　三角形ＡＣＲ：三角形ＡＣＰ＝ＲＨ：ＰＨ＝１：２

　　よって、

　　　三角形ＡＣＲ：（三角形ＡＰＲ＋三角形ＣＰＲ）＝１：１

　　これらの比から、 

　　　三角形ＡＰＲ：三角形ＣＰＲ：三角形ＡＣＲ＝１：１：２

　　次に、ＰＱ：ＣＱを求めます。　

　　　ＰＱ：ＣＱ＝三角形ＡＰＲ：三角形ＡＣＲ＝１：２

　　これから、三角形ＡＰＱが三角形ＡＣＰの面積のだとわかります。

　　　三角形ＡＰＱの面積＝三角形ＡＣＰの面積×

　　　　　　　　　　　　＝（８×８×）×

　　　　　　　　　　　　＝１０ｃm2


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１０ｃm2