＜問題＞

　次の図のように、長方形Ａと六角形Ｂが直線上ｌに並んでいて、Ａは毎秒１cmの速さで
直線ｌ上を矢印の方向に動きます。下のグラフは、ＡがＢに重なり始めてからの時間と、
重なりの部分の面積の関係を表したものです。これについて、次の問いに答えなさい。




　　


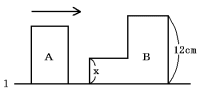
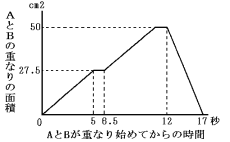
(1) 図のｘの長さは何cmですか。


(2) 六角形Ｂの面積は何ｃm2ですか。


(3) ＡとＢの重なりの部分の面積がはじめて３０ｃm2になるのは、ＡとＢが重なり始めて
　から何秒後ですか。















＜解答＞

(1) ＡとＢが重なり始めて５秒後には次の図のようになります。


　　


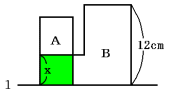
　　横の長さは、毎秒１cm×５秒＝５cm

　　面積はグラフから、２７．５ｃm2

　　よってｘの値は、

　　　２７．５÷５＝５．５cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　５．５cm


(2) ＡとＢが重なり始めて６．５秒後には次の上の図、１２秒後には次の下の図のように
　　なります。


　　

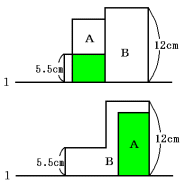
　　六角形Ｂを２つの長方形に分けて考えます。

　　上の図から、左側は縦５．５cm、横６．５cmとわかり、その面積は、

　　　５．５×６．５＝３５．７５ｃm2

　　右側は縦１２cm、横（１２−６．５＝）５．５cmとわかり、その面積は、

　　　１２×５．５＝６６ｃm2

　　Ｂ全体の面積は、

　　　３５．７５ｃm2＋６６ｃm2＝１０１．７５ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１０１．７５ｃm2


(3) ふつうはグラフから変化の割合を考えて求めます。

　　長方形Ａの横の長さは５cmなので重なりの面積が初めて５０ｃm2になるのは、

　　　６．５＋５＝１１．５秒後




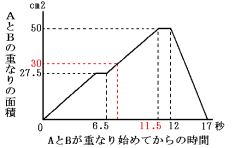
　　グラフから６．５秒から１１．５秒後までの５秒間に増えた面積は、

　　　５０−２７．５＝２２．５ｃm2　
　　
　　面積増加の割合は、

　　　２２．５÷５＝毎秒４．５ｃm2

　　面積が初めて３０ｃm2になったのは、

　　　６．５＋（３０−２７．５）÷４．５＝７秒後

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　７秒後