＜問題＞

　［図１］のように、底面の直径が４cm、ＯＡの長さが２４cmの円すいがあります。
［図２］、［図３］、［図４］のようにそれぞれ１本のひもで、ひもの長さがもっとも短
くなるように点Ａから点Ａまでまきつけます。このとき、次の各問いに答えなさい。
また、必要ならば、［図５］の三角形を利用しなさい。
　　　

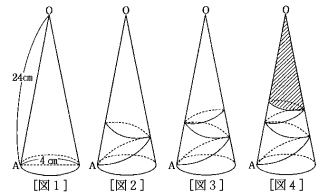
(1) ［図２］ではひもを２回まきつけてあります。
　　そのひもの長さを１辺とする正方形の面積を求めなさい。


(2) ［図３］ではひもを３回まきつけてあります。
　　そのひもの長さを１辺とする正方形の面積を求めなさい。


(3) ［図４］ではひもを４回まきつけてあります。円すいの側面のうち、１番上にあるひ
　もより上の斜線部分の面積を求めなさい。
　　ただし、答えは小数第２位を四捨五入して小数第１位まで求めなさい。















＜解答＞

(1) この円錐の側面の展開図にあたるおうぎ形の中心角は、

　　　３６０度×＝３０度

　　このひもは２回巻きつけあるので、中心角を２倍にしたおうぎ形で考える必要があり
　　ます。よって右下の図のように表されます。（図は正確ではありません）

　　　

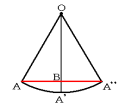
　　三角形ＯＡＡ''は正三角形なので、

　　　ひもの長さＡＡ''＝ＯＡ＝２４cmm

　　正方形の面積は、

　　　２４×２４＝５７６ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　５７６ｃm2


(2) 今度は３回巻きつけてあるので、中心角が９０度のおうぎ形で考えます。

　　それを４つまとめると次の図になります。　　




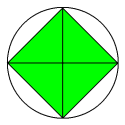
　　ひもの長さを１辺とする正方形は上の図の緑の正方形と同じものです。

　　円の半径がＯＡの２倍の４８cmにあたるので、　
　　
　　　正方形の面積＝４８×４８÷２＝１１５２ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１１５２ｃm2


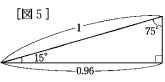
(3) 今度は４回巻きつけてあるので、中心角が１２０度のおうぎ形で考えます。

　　　　

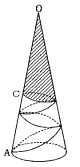
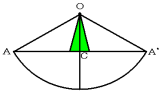
　　三角形ＯＡＣは３つの角が３０度、６０度、９０度の直角三角形なので、

　　　ＯＣの長さ＝ＯＡの長さ÷２＝１２cm

　　これより、斜線部分（展開図では緑色の二等辺三角形）は[図５]と相似な三角形２
　　つ分になります。




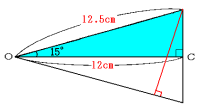
　　等しい辺の長さをｘcmとすると、

　　　ｘ：１２＝１：０．９６

　　　ｘ＝１２．５cm

　　等しい辺を底辺とすると高さは赤い線になります。３０度、６０度、９０度の直角三
　　角形の性質を使って、

　　　三角形の高さ＝１２．５÷２＝６．２５cm

　　　三角形の面積＝１２．５×６．２５÷２＝３９．６２５ｃm2

　　四捨五入して、３９．１ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３９．１ｃm2