＜問題＞
　次の図のように中心がＯの円があります。３点Ｐ、Ｑ、Ｒが同時にＡから出発し、それ
ぞれ一定の速さで円周上を動きます。点Ｐは時計回りに２分間で１周し、点Ｑは反時計回
りに３分間で１周します。点Ｒははじめ反時計回りに、その後時計回りにと、一定の時間
ごとに向きを変えることを繰り返します。


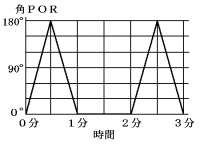
　線ＯＰと線ＯＲにはさまれたせまい方の角（１８０°以下）を角ＰＯＲとします。
　角ＰＯＲの大きさと時間の関係は次のグラフのようになりました。


　このとき、次の問いに答えなさい。

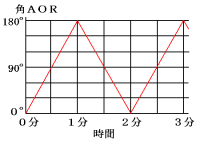
(1) 角ＡＯＲの大きさと時間の関係のグラフをかきなさい。




(2) 初めて角ＱＯＲが１８０°になるのは何分何秒後ですか。















＜解答＞

(1) グラフから点Ｒは１分間反時計回りに動き、その後の１分間時計回りに動くことがわ
　　かります。

　　速さは、点ＰとＲが等しく、

　　　３６０度÷２分＝毎分１８０度

　　よって、次のグラフで表されます。　




(2) 点Ｑの速さは、

　　　３６０度÷３分＝毎分１２０度

　　２点Ｑ、Ｒが同じ方向に進むときに、

　　　１８０−１２０＝毎分６０度

　　この速さで角ＱＯＲの大きさが増えたり減ったりします。

　　２点Ｑ、Ｒが反対方向に進むときに、

　　　１８０＋１２０＝毎分３００度

　　この速さで角ＱＯＲの大きさが増えたり減ったりします。

　　これをもとに１分ごとに調べていくのが普通です。ここではわかりやすくグラフを書
　　いてみましょう。角ＱＯＲの大きさの変化は次のグラフのようになります。



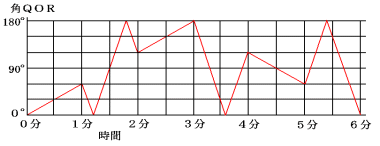
　　初めて１８０度になるのは、１分後から２分後の間です。

　　角が６０度から０になるのに、

　　　６０÷３００＝０．２分

　　そこから１８０度になるのに、

　　　１８０÷３００＝０．６分

　　よって、

　　　１＋０．２＋０．６＝１．８分後＝１分４８秒後

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１分４８秒後