＜問題＞

　図のように直角三角形ＡＢＣを平行に移動した後で、点Ｆを中心に９０°回転させまし
た。円周率を３．１４として、次の問いに答えなさい。


　
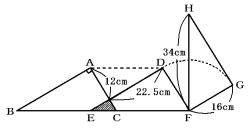
(1) 斜線の部分の面積は何ｃm2ですか。


(2) 何ｃｍ平行移動させましたか。


(3) ９０°の回転移動で辺ＤＥが動いたあとの図形の面積は何ｃm2ですか。















＜解答＞

(1) ＡＣとＤＥの交点をＩとすると、

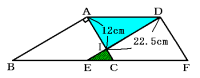
　　三角形ＡＩＤと三角形ＣＩＥは相似な直角三角形です。
　　
　　　ＣＩ＝１６cm−１２cm＝４cm

　　　ＤＩ：ＥＩ＝ＡＩ：ＣＩ
　　　　　　　　＝１２cm：４cm
　　　　　　　　＝３：１

　　　ＥＩ＝２２．５cm×＝７．５cm

　　三角形ＡＩＤの面積は、

　　　７．５×４÷２＝１５ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１５ｃm2


(2) 平行移動させた距離はＡＤの長さと同じです。

　　三角形ＡＩＤと三角形ＣＡＢは相似なので、

　　　ＡＤ：ＣＢ＝ＡＩ：ＣＡ
　　　　　　　　＝１２cm：１６cm
　　　　　　　　＝３：４

　　　ＡＤ＝３４cm×＝２５．５cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　２５．５cm


(3) 辺ＤＥが動いたあとの図形は次図のアとイを組み合わせた部分（緑）です。


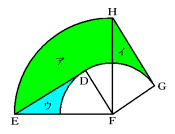
　　イの部分はウの部分（青）と合同なので、面積をアとウの和として求めることができ
　　ます。

　　　３４×３４×３．１４×−１６×１６×３．１４×

　　　＝３．１４×（２８９−６４）
　　　＝７０６．５ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　７０６．５ｃm2