＜問題＞

　答えだけでなく、途中の計算、式、図なども書きなさい。

　図のような二重の観覧車があり、すべての箱は等間隔で並んでいます。外側の観覧車は
時計とは逆回りに１周１６分、内側の観覧車は時計回りに１周１２分で回っています。今、
Ａ君、Ｂ君、Ｃ君の３人が図の位置にある箱に乗っています。

　
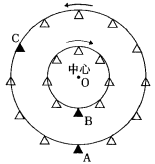
　次の問いに答えなさい。

(1) Ａ君、Ｂ君の位置と、観覧車の中心Ｏの３つが、はじめて一直線上に並ぶのは、今か
　ら何分後ですか。


(2) Ａ君が今から２周する間に、内側の観覧車の箱と何回すれ違いますか。


(3) この観覧車では、ある箱に乗った人から見える範囲が限られています。図１の（あ）
　の角のように、９０°以下ならばＥからＤは見えますが、図２の（い）の角のように、
　９０°をこえると見えなくなります。


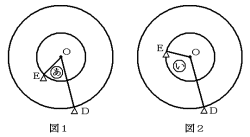
　今から１時間のうちに、Ｂ君からＡ君、Ｃ君の２人とも見えるのは何分間ですか。















＜解答＞

(1) 同じ円周上にはありませんが、旅人算（時計算）の考え方を利用して解くことができ
　　ます。

　　考えやすいようにＡ君の乗った箱、Ｂ君の乗った箱をそれぞれ点Ａ、Ｂと表します。

　　　点Ａの速さ　３６０度÷１６分＝毎分２２．５度
　　　点Ｂの速さ　３６０度÷１２分＝毎分３０度

　　３点Ｏ、Ａ、Ｂが一直線上に並ぶのは、角ＡＯＢ＝０度または１８０度のときです。

　　角ＡＯＢ＝０度の場合は、両方あわせて３６０度進んだときで、角ＡＯＢ＝１８０度
　　の場合は、両方あわせて１８０度進んだときです。早い方を考えて、　

　　　１８０度÷（毎分２２．５度＋毎分３０度）＝３分

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３分


(2) 内側の観覧車に８つの箱があるので、

　　　３６０度÷８＝４５度

　　４５度の間隔で箱があります。

　　　４５度÷（毎分２２．５度＋毎分３０度）＝分

　　Ａ君は分間隔で内側の観覧車の箱とすれ違います。

　　　１６分×２÷分＝３７回

　　よって３７回

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３７回


(3) 周期算の問題です。

　　内側の観覧車を固定して考えたときの外側の観覧車の進む速さは、反時計回りで毎分
　　５２．５度です。

　　Ａ君の箱が見えるのは、次の図の範囲で、


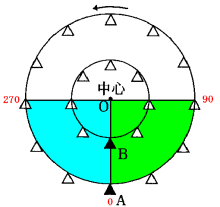
　　　９０÷５２．５＝１分

　　　２７０÷５２．５＝５分

　　　３６０÷５２．５＝６分

　　Ａ君の箱が見えるのは、１周の間では０分〜１分、５分〜６分です。

　　Ｂ君の箱が見えるのは、次の図の範囲で、


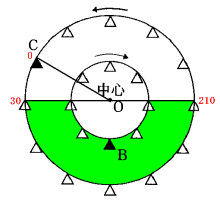
　　　　３０÷５２．５＝分

　　　　２１０÷５２．５＝４分

　　　Ｃ君の箱が見えるのは、１周の間では分〜４分です。

　　　両方に共通するのは、分〜１分です。

　　　６０分間に観覧車は、

　　　　６０÷６＝８回転あまり５分

　　　したがってＡ君、Ｃ君が両方とも見える時間は、

　　　　（１−）×９＝１０分間

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１０分間