＜問題＞

　図のように、空き地に横幅が２ｍの看板が立ててあります。看板は北側の塀から１ｍ離
れた場所に、北側の塀と平行に立てられています。Ａ、Ｂの２地点は北側の塀の長さを直
径とする半円周上にあり、この半円の中心をＯ、両端の点をそれぞれ、Ｃ、Ｄとしていま
す。この看板に、Ａ地点からライトの光を当て、北側の塀にできた影の横幅を測ったとこ
ろ２．４ｍでした。また、影の右端はＯ地点と重なっています。

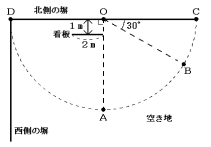
(1) 北側の塀の長さは、何ｍですか。


(2) Ｂ地点からライトの光を当てると、北側の塀にだけ影ができました。影の横幅は、何
　　ｍですか。


(3) Ｃ地点からライトの光を当てると、西側の塀に影ができました。影の横幅は、何ｍで
　　すか。
















＜解答＞

(1) 図のように２つの三角形ＡＰＱとＡＯＲとの相似を考え、半円の半径を求めます。

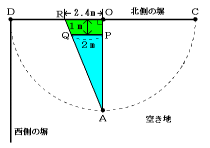
　　この２つの三角形の相似比は、

　　　ＰＱ：ＯＲ＝２ｍ：２．４ｍ
　　　　　　　　＝５：６

　　ＡＰ：ＡＯ＝５：６から、

　　　ＡＯ＝１ｍ×＝６ｍ

　　北側の塀ＣＤの長さはＡＯの２倍なので、

　　　６ｍ×２＝１２ｍ

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１２ｍ


(2) 図のように２つの三角形ＢＰＱとＢＳＴとの相似を考えます。

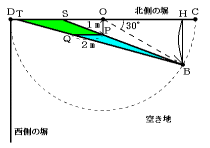
　　３０度、６０度、９０度の直角三角形の辺の関係から、

　　　ＢＨ＝ＯＢ×＝３ｍ

　　２つの三角形ＢＰＱとＢＳＴとの相似比は、

　　　（ＢＨ−ＰＯ）：ＢＨ＝（３ｍ−１ｍ）：３ｍ
　　　　　　　　　　　　　＝２：３

　　ＰＱ：ＳＴ＝２：３から、影の幅ＳＴの長さを求めます。

　　　２ｍ×＝３ｍ

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３ｍ


(3) 図ように２つの三角形ＣＰＵとＣＶＷとの相似を考えて求めます。

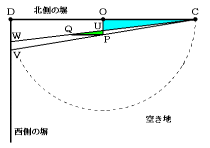
　　ＰＵの長さを求めることが必要です。そこで最初に２つの三角形ＯＣＵとＰＱＵと
　　の相似を考えます。

　　この２つの三角形の相似比は、

　　　ＯＣ：ＰＱ＝６ｍ：２ｍ
　　　　　　　　＝３：１

　　ＯＵ：ＰＵ＝３：１でＯＰ＝１ｍだから、

　　　ＰＵ＝１ｍ×＝ｍ

　　次に、２つの三角形ＣＰＵとＣＶＷとの相似を考えます。

　　この２つの三角形の相似比は、

　　　ＣＯ：ＣＤ＝６ｍ：１２ｍ
　　　　　　　　＝１：２

　　ＰＵ：ＶＷ＝１：２から、影の幅ＶＷを求めます。

　　　ＶＷ＝ｍ×２＝ｍ

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　ｍ