＜問題＞

　次の図は正方形ＡＢＣＤと、直角三角形ＡＥＢを組み合わせたものです。このとき、
次の各問いに答えなさい。　　　　＊表記の都合上、問題文の一部を変えてあります。

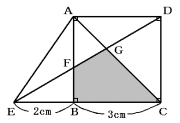
(1) ＥＦ：ＦＧ：ＧＤを、もっとも簡単な整数比で答えなさい。


(2) ＡＦの長さを求めなさい。


(3) 影の部分、四角形ＦＢＣＧの面積を求めなさい。

















＜解答＞

(1) 連比をつくるには相似な三角形を２組考える必要があります。

　　ここでは、三角形ＥＦＢと三角形ＤＦＡの組と三角形ＥＧＣと三角形ＤＧＡの組を
　　考えていきます。


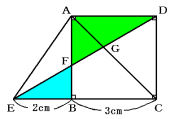
　　三角形ＥＦＢと三角形ＤＦＡで相似比は、

　　　ＥＢ：ＤＡ＝２cm：３cm

　　　　　　　　＝２：３

　　ＥＦ：ＤＦ＝２：３です。ＥＤの長さ全体を１とすると、

　　　ＥＦ＝、ＤＦ＝　　　


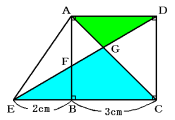
　　三角形ＥＧＣと三角形ＤＧＡで相似比は、

　　　ＥＣ：ＤＡ＝（２cm＋３cm）：３cm

　　　　　　　　＝５：３

　　ＥＧ：ＤＧ＝５：３です。ＥＤの長さ全体を１とすると、

　　　ＤＧ＝

　　　ＦＧ＝ＤＦ−ＤＧ

　　　　　＝−

　　　　　＝

　　よって、

　　　ＥＦ：ＦＧ：ＧＤ＝：：

　　　　　　　　　　　＝１６：９：１５

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１６：９：１５


(2) 三角形ＥＦＢと三角形ＤＦＡとの相似で考えて、

　　　ＢＦ：ＡＦ＝２：３

　　ＡＦ＝３cm×＝１cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１cm


(3) いろいろな考え方があります。ここでは「高さの等しい三角形の面積の比は底辺の
　　長さの比に等しい」という考え方を用いています。

　　三角形ＡＥＣの面積は、

　　　５×３×＝７ｃm2

　　三角形ＥＣＧと三角形ＤＧＡの相似比から、

　　　ＣＧ：ＡＧ＝５：３

　　三角形ＥＣＧの面積は、「高さの等しい三角形の面積の比は底辺の長さの比に等し
　　い」ことを使って、

　　　７×＝４ｃm2

　　また三角形ＥＢＦの面積は、

　　　２cm×（３cm−１cm）×＝１ｃm2

　　よって四角形ＦＢＣＧの面積は、

　　　三角形ＥＣＧの面積−三角形ＥＢＦの面積

　　　＝４ｃm2−１ｃm2

　　　＝３ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３ｃm2