<問題>
次の図のように、太線で4つにくぎられたところに折れ線を引き、1から順に奇数を
入れていきます。次の問いに答えなさい。
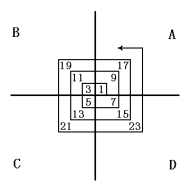
(1) 101はA、B、C、Dのどの部分に入りますか。理由も15字程度で書きなさい。
(2) Bの部分の数を、ある数から大きくなる順にいくつかたしていくと、440になり
ます。ある数はいくつですか。
<解答>
(1) 奇数を4つのグループに分けることになります。次の表のようにそれぞれの場所に
入る数を順に書いていくと、等差数列ができます。
| A | 1 | 9 | 17 | 25 | 33 | ・・・ |
| B | 3 | 11 | 19 | 27 | 35 | ・・・ |
| C | 5 | 13 | 21 | 29 | 37 | ・・・ |
| D | 7 | 15 | 23 | 31 | 39 | ・・・ |
それぞれの数の特徴は、次の通りです。
A:8で割ると1余る整数
B:8で割ると3余る整数
C:8で割ると5余る整数
D:8で割ると7余る整数
「101÷8=12余り5」なので、Cに入ります。
答 C、(理由)8で割ると5余る整数だから。
(2) 「等差数列の和」の公式をそのまま使って解くことはできません
等差数列の和=(最初の数+最後の数)×数の個数÷2 なので、
「(最初の数+最後の数)×数の個数」のところに目を付けます。
440×2=880 なので、
(最初の数+最後の数)と数の個数はともに880の約数
また、最初の数、最後の数はともに「8の倍数+3」になので、
(最初の数+最後の数)は8の倍数+6・・・(ア)
880の約数で条件(ア)に当てはまるものは、110だけです。
最初の数+最後の数=110
数の個数=8
数の個数が8なので、
最後の数−最初の数=8×(8−1)=56
和差算の考え方を使って、
最初の数=(110−56)÷2=27
答 27
*他にも考え方があります。上では約数の性質を用いた考え方を使いました。