<問題>
次の<図1>で点Aから,次のようなルールにしたがって点が動いています。
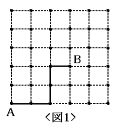
【ルール】 ①Aを出発するとき,自分で決めた点数を持っています。 ②点数が偶数のときには右に1目もり動きます。そのとき,持っている点数は半分に なります。 ③点数が奇数のときは上に1目もり動きます。そのとき,持っている点数は1をたし てから2で割った点数になります。 ④点数が1点になったら終わりです。 |
たとえば,はじめの点数が20点のとき,点数の変化は20→10→5→3→2→1と
なって,上の<図1>の点Bに到着します。
次の問いに答えなさい。
(1) はじめの点数が42点のとき,到着するまでの道順を<図1>にならって矢印で示し
なさい。

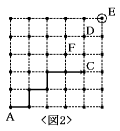
(2) <図2>のような道を通って点Cに到着したときの,はじめの点数を求めなさい。
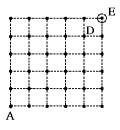
(3) <図2>の点Dに到着したとき,点Eは通ることができない点です。通ることができ
ない残りのすべての点を,○で囲みなさい。
(4) 出発してから到着するまでに3目もり動いたとき,はじめの点数は何点以上何点以下
でしたか。
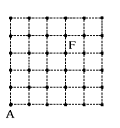
(5) <図2>の点Fに到着したとき,はじめの点数は何通りの場合が考えられますか。
また,そのとき考えられる最も小さい点数と最も大きい点数を求めなさい(式や考え
方も書きなさい)。
<解答>
(1) 実際に計算して決めていきます。
42 →
42÷2=21 ↑
(21+1)÷2=11 ↑
(11+1)÷2=6 →
6÷2=3 ↑
(3+1)÷2=2 →
2÷2=1 終
これを図に表すと次のようになります。
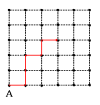
(2) 逆に計算していきます。
移動を逆に考えると、
ア:左方向に戻った数を求めるには、わかっている数を2倍する
イ:下方向に戻った数を求めるには、わかっている数を2倍して1を引く
これから、
1×2=2
2×2=4
4×2-1=7
7×2=14
14×2-1=27
27×2=54
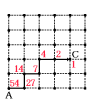 答 54点
答 54点(3) 条件から、Dの左隣は2に決まります。
移動を逆に考えると、もとが1以外ならば (2)のアとイのどちらの方法も可能です。
よって、答は次のようになります。
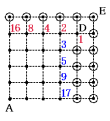
(4) 上のように最後の計算は、必ず「2÷2=1」に決まります。
もとの数を求める作業では、上の(2)のアの方が数が大きくなり、イの方が小さくな
ります。
2から逆に残る2つの動きを考えて、
みなアの場合、 2×2=4
4×2=8
みなイの場合、 2×2-1=3
3×2-1=5
よって、はじめの点数は、5以上8以下だとわかります。
答 5以上8以下
(5) Fの左隣の2から考えると、Aの位置に戻るのには、アを2度、イを3度行う必要が
あります。
また、アとイの並び方がちがうとできる数が異なります。
全部で5度の作業のうち、イの作業2度が何度目に入るかを考えて数えることができ
ます。組み合わせの考え方を使って求めることができます。
5×4÷2=10
最初の点数は10通りです。
また、ア・イを1度ずつ行う場合でも、アを先に行う方が数が大きくなります。
ア→イの順 2×2=4、4×2-1=7
イ→アの順 2×2-1=3、3×2=6
これから考えて、
最大の点数 2×2=4
4×2=8
8×2-1=15
15×2-1=29
29×2-1=57
最小の点数 2×2-1=3
3×2-1=5
5×2-1=9
9×2=18
18×2=36
答 10通り、最大の数:57、最小の数:36