次の〔図1〕のような三角柱の容器の中に水が入っているとき、次の問いに答えなさい。
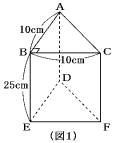
(1) 〔図1〕で水面の高さを測ったら、16cmでした。このとき、三角柱を〔図2〕のよ
うに置いたら、PBの長さは、何cmになりますか。
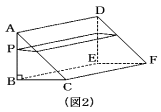
(2) 〔図1〕で水面の高さを測ったら20cmでした。このとき、EDを床につけたまま、
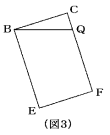
〔図3〕のように傾けたら、QFの長さは何cmになりますか。
式をかいて答えなさい。
<解答>
(1) 次のように水が入っていない部分は三角柱になります。
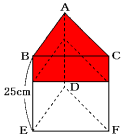
水が入っていない部分の体積と容器全体の体積比は、
(25−16):25=9:25
次のように〔図2〕で三角形ABCを底面に考えると、
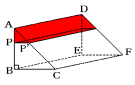
水が入っていない部分の底面は三角形APP’です。
この三角形APP’と三角形ABCと相似で、面積比は9:25です。
9:25=(3×3):(5×5)
これより、相似比が3:5とわかります。
AP=10×=6cm
答 6cm
(2) 〔図1〕の置き方で水が入っていない部分は三角柱で、底面を三角形ABCとすると、
高さは4cmです。

〔図3〕の置き方で水が入っていない部分は三角錐で、底辺を三角形ABCとすると、
高さは辺CQとなります。
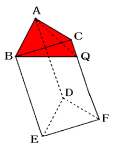
体積と底面積がお互いに等しい柱体と錐体を比べると、錐体の高さは柱体の高さの3
倍なので、
CQ=(25−20)×3=15cm
これから、
QF=25−15=10cm
答 10cm