<問題>
次の図のような、ひし形ABCDの周りにそって,図形をすべらせないように1周転が
します。次の問いに答えなさい。
ただし,円周率は3とします。(式または考え方も書きなさい)
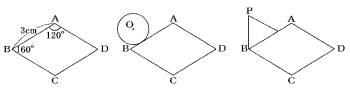
(1) 周の長さが3cmである円を転がすとき,円の中心Oの動いた道のりを求めなさい。
(2) 一辺の長さが2cmである正三角形を転がすとき,頂点Pの動いた道のりを求めなさい。
<解答>
(1) 中心の動いた跡は次のようになります。
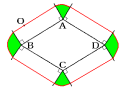
図の直線部分はおうぎ形ABCDの周に等しいので,
3×4=12cm
4つのおうぎ形の中心角を求めると,
大きい2つ 360−90×2−60=120度
小さい2つ 360−90×2−120=60度
4つ合わせると,
120×2+60×2=360度
*凹みのない三角形や多角形の周りを1周するときには,角にできた中心角の和が
360度になることは覚えておくと良いでしょう。
円Oは周の長さが3cmなので,円Oの直径は,
3÷3=1cm
曲線部分の長さの和は,
1×3=3cm
よって,
12+3=15cm
答 15cm
(2) 頂点P動いた跡は次のようになります。
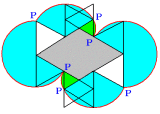
3組の合同なおうぎ形の弧になり,半径と中心角はそれぞれ,
(2cm,120度),(2cm,240度),(1cm、60度) です。
点Pの動いた道のりは,
2×2×3×
答 26cm