図のように,円すいを切って,2つの立体ア,イに分けるとき,次の各問いに答えなさ
い。ただし,円周率は3.14とします。
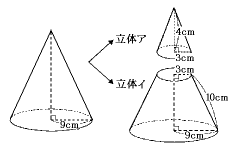
(1) 立体アの太線の部分の長さは何cmですか
(2) 立体アの表面積は何cm2ですか。
(3) 立体アと立体イの表面積の比を求めなさい。
<解答>
(1) 次の図で赤い部分は直角三角形です。
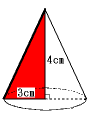
この図の直角三角形は3辺の長さの比が3:4:5のものです。
これより,図の太線の部分はの長さは5cmです。
答 5cm
*直角三角形の辺の比のうち,3つとも整数になるものを「ピタゴラス数」と呼びま
す。入試問題を作成する時に参考して作ることが多いので,それらのうちで以下の
組み合わせは覚えておくと良いでしょう。
(3:4:5),(5:12:13),(7:24:25),(8:15:17)
(2) 立体アは円錐です。
「円錐の側面積=底面の半径×母線×円周率」を用いて考えます。
立体アの表面積は,
底面積+側面積=3×3×3.14+3×5×3.14
=(9+15)×3.14
=24×3.14
=75.36cm2
答 75.36cm2
(3) 立体イの展開図を考えると,次のようになります。
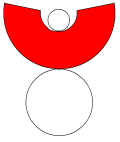
側面に当たる赤い面は,もとの円錐の側面から立体アの側面を除いたものです。
側面積=9×(5+10)×3.14−3×5×3.14
=(135−15)×3.14
=120×3.14
表面積=上の底面積+下の底面積+側面積
=3×3×3.14+9×9×3.14+120×3.14
=(9+81+120)×3.14
=210×3.14
立体アと立体イの表面積の比は,
(24×3.14):(210×3.14)=24:210
=4:35
答 4:35
*すべて3.14かけて求めるので,最初から3.14を消して考えても良いでしょ
う。