＜問題＞

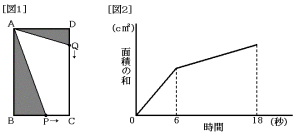
　次の［図１］のような，辺ＡＢの長さが３６cmの長方形ＡＢＣＤがあります。点Ｐは頂
点Ｂを出発し，辺ＢＣ，ＣＤ上を矢印の向きに，一定の速さで頂点Ｄまで休まず動きます。
また，点Ｑは頂点Ｄを出発し，辺ＤＣ上を矢印の向きに，点Ｐのの速さで頂点Ｃまで休ま
ず動きます。２点Ｐ，Ｑはそれぞれ頂点Ｂ，Ｄを同時に出発し，点Ｑが頂点Ｃに着くより
も早く，点Ｐは頂点Ｄに着きました。[図２]は，２点Ｐ，Ｑが同時に出発してからの時間
（秒）と，そのときの三角形ＡＢＰの面積と三角形ＡＤＱの面積の和(ｃm2)との関係を，
点Ｑが頂点Ｃに着くまで表したグラフです。これについて，下の各問いに答えなさい。途
中の計算式も書きなさい。

　　　　
(1) 点Ｐが頂点Ｄに着くのは，２点Ｐ，Ｑが同時に出発してから何秒後ですか。


(2) ２点Ｐ，Ｑが同時に出発してからｘ秒後の，三角形ＡＢＰの面積と三角形ＡＤＱの面
　積の和をｙｃm2とします。２点Ｐ，Ｑが同時に出発してから６秒後までのｘとｙの関係
　を表す式を求めなさい。


(3) ２点Ｐ，Ｑが同時に出発してから１２秒後の，三角形ＡＢＰと三角形ＡＤＱが重なる
　部分の面積を求めなさい。















＜解答＞

(1) ２つの三角形の面積の変化を考えます。

　　ア）三角形ＡＢＰの面積

　　　　点Ｐが辺ＢＣ上にあるとき　…　一定の割合で増える

　　　　点Ｐが辺ＣＤ上にあるとき　…　長方形ＡＢＣＤの面積の半分で変わらない

　　　　

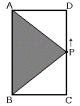
　　イ）三角形ＡＤＱの面積

　　　　点Ｑが辺ＤＣ上にあるとき　…　一定の割合で増える

　　このことを考えてグラフを見ると，面積の和の増え方が変わった６秒後に点Ｐが頂点
　　Ｃを通過したことがわかります。また，点Ｑは辺ＤＣを１８秒かけて動いたこともわ
　　かります。

　　点Ｐの速さは点Ｑの２倍なので，点Ｐが辺ＣＤ上を動くのにかかる時間は，

　　　１８秒÷２＝９秒

　　よって，点Ｐが頂点Ｄに着いたのは，

　　　６秒＋９秒＝１５秒

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１５秒後


(2) 点Ｑは辺ＤＣを１８秒かけて動いたので，点Ｑの速さは，

　　　３６cm÷１８秒＝毎秒２cm

　　点Ｐの速さは点Ｑの速さの２倍なので，

　　　毎秒２cm×２＝毎秒４cm

　　点Ｐは辺ＢＣ上を動くのに６秒かかっているので，辺ＢＣの長さは，

　　　毎秒４cm×６秒＝２４cm

　　三角形ＡＢＰの面積をｘを用いて表すと，

　　　３６cm×（毎秒４cm×ｘ秒）÷２＝７２×ｘｃm2

　　同様に三角形ＡＤＱの面積をｘを用いて表すと，

　　　２４cm×（毎秒２cm×ｘ秒）÷２＝２４×ｘｃm2

　　よって，

　　　ｙ＝７２×ｘ＋２４×ｘ
　　　　＝９６×ｘ

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　ｙ＝９６×ｘ


(3) 次の図の赤い三角形ＡＰＲが重なりの部分です。

　　　　

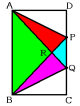
　　まず，１２秒後の２点Ｐ，Ｑの位置を考えます。

　　ＰＤの長さは，点Ｐが１５秒後に頂点Ｄに着くことを利用して，

　　　毎秒４cm×（１５秒−１２秒）＝１２cm

　　ＤＱの長さは点Ｑが１２秒間に動いた距離になるので，

　　　毎秒２cm×１２秒＝２４cm

　　よって，１２秒後のＱＰの長さは，

　　　２４cm−１２cm＝１２cm

　　また，三角形ＡＢＲと三角形ＱＰＲは相似です。

　　相似比を求めると，

　　　ＡＢ：ＱＰ＝３６cm：１２cm
　　　　　　　　＝３：１

　　色が塗られた４つの三角形の面積比を求めると，

　　相似形の面積比から，

　　　三角形ＡＢＲ：三角形ＱＰＲ＝（３×３）：（１×１）
　　　　　　　　　　　　　　　　＝９：１

　　高さが等しい三角形の面積比から，

　　　三角形ＱＰＲ：三角形ＡＰＲ：三角形ＢＱＲ＝１：３：３

　　よって，

　　　三角形ＡＢＲ：三角形ＱＰＲ：三角形ＡＰＲ：三角形ＢＱＲ＝９：１：３：３

　　また，台形ＡＢＱＰの面積は，

　　　（３６cm＋１２cm）×２４cm÷２＝５７６ｃm2

　　三角形ＡＰＲの面積は，

　　　５７６ｃm2×＝１０８ｃm2


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１０８ｃm2