算数

　　　　「三角形の個数を考える問題」

　　　　約束記号の問題は最初から計算式が示されるのが一般的ですが，この問題は計算法が図形
　　　　で示されています。図形をもとに計算の規則を考える方法もありますが，ここでは平方数
　　　　の数列の考え方を使って解きます。平方数の数列では隣り合った数の差を考える問題が出
　　　　されることが多いので，その計算法も覚えておきましょう。

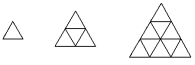
＜問題＞ 　１辺の長さ１cmの正三角形を△とします。１辺の長さ２cmの正三角形の中には，△が４ 個含まれています。これを，<２>＝４で表すことにします。１辺の長さ３cmの正三角形な らば，△が９個含まれていますから，<３>＝９になります。次の問いに答えなさい。 　　　　 (1) <５>はいくつですか。 (2) <１３>−<１２>はいくつですか。 (3) <◆＋１>−<◆>＝９９のとき，はいくつですか。 　　＊表記の都合で一部変えたところがあります。 ＜解答＞ (1) 正三角形の１辺がＮcmの場合，相似形の面積比を利用すると，１辺が１cmの正三角形 　　の個数はＮ×Ｎ個になることがわかります。 　　<Ｎ>＝Ｎ×Ｎなので， 　　　<５>＝５×５ 　　　　　＝２５ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　２５ (2) 上の規則を用いて計算します。 　　　<１３>−<１２>＝１３×１３−１２×１２ 　　　　　　　　　　＝１６９−１４４ 　　　　　　　　　　＝２５ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　２５ (3) <Ｎ>を小さい順に並べると次のような平方数の数列になります。 　　｛１，４，９，１６，２５，…｝ 　　次の図のように正方形のます目の数で考えると， 　　青色の正方形の数がＮ×Ｎです。 　　それに１列，緑と赤の正方形を加えると，（Ｎ＋１）×（Ｎ＋１）です。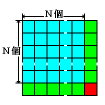 　　　　 　　これより，隣り合う平方数の差は，緑の正方形の個数（Ｎ×２）個と赤い正 　　方形１個との合計で表されるとがわかります。 　　よって，その差は（Ｎ×２＋１）個です。 　　これを使って， 　　　◆×２＋１＝９９ 　　　◆＝（９９−１）÷２ 　　　　＝４９ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 答　４９ 　　＊この計算法「（Ｎ＋１）×（Ｎ＋１）−Ｎ×Ｎ＝Ｎ×２＋１」を使うと， 　　　(２)も次のように求めることができます。 　　　　<１３>−<１２>＝１２×２＋１＝２５

ページTopへ