次の図1のような水そうに,1分間に24リットルの割合で水を入れます。水を入れな
がら途中で,図2の立体を傾けずにゆっくり一定の速さで水そうに入れて,その底面が水
そうの底に着くまで下しました。そして,水そうが満水になるまで水を入れ続けました。
この水そうの水の深さのようすをグラフに表すと,図3のようになりました。
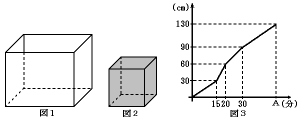
(1) 図1の水そうの底面積は何cm2ですか。
(2) 図3のAは何分を表していますか。
(3) 図2の立体の体積は何cm3ですか。
<解答>
グラフに表された水の深さの変化の割合をもとに時間を区切って様子を考えると、
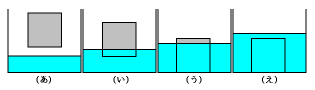
(あ) 0〜15分…立体は水の中に入ってはいません
(い)15〜20分…立体は一部が水の中ですが、水そうの底には達していません
(う)20〜30分…立体は水そうの底に達していますが、一部が水面の上にあります
(え)30〜(A)分…立体は完全に水の中に入っています
(1) 水を入れ始めて15分後から水の深さの変化の割合が増しているので、この時から立
体が水の中に沈んでいくと考えられます。
15分までに水そうにたまった水の体積から容器の底面積を考えます。
24リットル=24000cm3なので、
毎分24000cm3×15分÷30cm=12000cm2
答 12000cm2
(2) 水を入れ始めて30分後からは立体が完全に水中に沈んでしまった考えられるので、
水の深さの変化の割合は15分までと同じになります。
水の深さの変化の割合は、
30cm÷15分=毎分2cm
水の深さが90cmから130cmになるのにかかった時間は、
(130cm−90cm)÷毎分2cm=20分
よって、Aのは、
30分+20分=50分
答 50分
(3) 水そうの容積は、
12000cm2×130cm=1560000cm3
一杯になるまでに入った水の体積は、
毎分24000cm3×50分=1200000cm3
この2つの量の差が立体の体積にあたるので、
1560000cm3−1200000cm3=360000cm3
答 360000cm3