＜問題＞

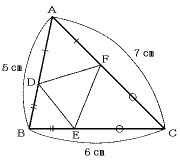
　ＡＢ，ＢＣ，ＣＡの長さが，それぞれ５cm，６cm，７cmの三角形ＡＢＣがあります。
ＡＢ，ＢＣ，ＣＡの各辺上に，点Ｄ，Ｅ，ＦをＡＤとＡＦ，ＢＤとＢＥ，ＣＥとＣＦの長
さがそれぞれ等しくなるように，図のようにとります（同じ印は，長さが等しいことを表
します）
　　　　

(1) ＡＤ＋ＢＥ＋ＣＦの長さを求めなさい。


(2) ＡＤ，ＢＥ，ＣＦの長さをそれぞれ求めなさい。


(3) 三角形ＡＤＦの面積は，三角形ＡＢＣの面積の何倍ですか。


(4) 三角形ＤＥＦの面積は，三角形ＡＢＣの面積の何倍ですか。















＜解答＞

＊３辺の長さの和と各辺の長さを文字で表すと式がわかりやすくなります。

(1) ＡＤ＝ＡＦ＝ａ，ＢＤ＝ＢＥ＝ｂ，ＣＥ＝ＣＦ＝ｃとすると、

　　　ＡＢ＋ＢＣ＋ＣＡ＝（ａ＋ｂ）＋（ｂ＋ｃ）＋（ｃ＋ａ）
　　　　　　　　　　　＝（ａ＋ｂ＋ｃ）×２

　　また、

　　　ＡＢ＋ＢＣ＋ＣＡ＝５cm＋６cm＋７cm＝１８cm

　　ＡＤ＋ＢＥ＋ＣＦ＝ａ＋ｂ＋ｃ　だから、

　　　ａ＋ｂ＋ｃ＝１８cm÷２＝９cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　９cm


(2) (１)より、

　　　ａ＋ｂ＋ｃ＝９cm

　　また、

　　　ａ＋ｂ＝５cm　ｂ＋ｃ＝６cm　ｃ＋ａ＝７cm

　　これらから、

　　　ａ＝（ａ＋ｂ＋ｃ）−（ｂ＋ｃ）
　　　　＝９cm−６cm
　　　　＝３cm

　　　ｂ＝（ａ＋ｂ＋ｃ）−（ｃ＋ａ）
　　　　＝９cm−７cm
　　　　＝２cm

　　　ｃ＝（ａ＋ｂ＋ｃ）−（ａ＋ｂ）
　　　　＝９cm−５cm
　　　　＝４cm

　　　　　　　　　　　　　　　　　　　　　答　ＡＤ＝３cm、ＢＥ＝２cm、ＣＦ＝４cm

　＊この計算法は、３つの量のうちで２つずつの和が分っているときに、それぞれの量を
　　を求める時に使われるものです。必ず覚えておきましょう。


(3) ２つの三角形で１つの角がお互いに等しい時、その面積比は等しい角をはさむ２つの
　　辺の長さの積の比で求めることができます。

　　　　

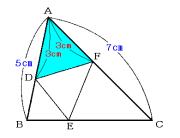
　　三角形ＡＤＦと三角形ＡＢＣでは、角Ａが共通なのでその面積比は、

　　　（ＡＤ×ＡＦ）：（ＡＢ×ＡＣ）＝（３×３）：（５×７）
　　　　　　　　　　　　　　　　　　＝９：３５

　　これから、

　　　９÷３５＝

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　倍　


(4) 三角形ＤＥＦと三角形ＡＢＣの面積比は直接求めることはできませんが、(３)の方法
　　を用いて、３つの三角形ＡＤＦ、ＢＥＤ、ＣＦＥがそれぞれ三角形ＡＢＣの何倍の面
　　積を持つかを考えると求めることができます。

　　まず、

　　　（ＢＥ×ＢＤ）：（ＢＣ×ＢＡ）＝（２×２）：（６×５）
　　　　　　　　　　　　　　　　　　＝２：１５

　　これから、三角形ＢＥＤは三角形ＡＢＣの倍の面積だとわかります。

　　次に、

　　　（ＣＦ×ＣＥ）：（ＣＡ×ＣＢ）＝（４×４）：（７×６）
　　　　　　　　　　　　　　　　　　＝８：２１

　　これから、三角形ＣＦＥは三角形ＡＢＣの倍の面積だとわかります。

　　三角形ＤＥＦは、三角形ＡＢＣから３つの三角形ＡＤＦ、ＢＥＤ、ＣＦＥを除いたも
　　のなので、

　　　１−（＋＋）＝

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　倍