＜問題＞

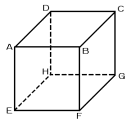
　白色と赤色の同じ大きさの立方体を積み重ねて大きな立方体を作りました。
図のように大きな立方体の対角線（図のＡＧ，ＢＨ，ＣＥ，ＤＦの直線）が通る小さな
立方体はすべて赤色で，その他の小さな立方体はすべて白色でした。
　次の問いに答えなさい。
　　　　
(1) 小さな立方体を２７個使って大きな立方体を作るとき赤色の小さな立方体は何個あり
　　ますか。


(2) 小さな立方体を６４個使って大きな立方体を作るとき赤色の小さな立方体は何個あり
　　ますか。


(3) 赤色の小さな立方体の数が１７個のとき，白色の小さな立方体は何個ありますか。


(4) 赤色の小さな立方体の数が２４個のとき，白色の小さな立方体は何個ありますか。















＜解答＞

＊大きな立方体の対角線と赤色の小さい立方体の対角線は重なります。

(1) ２７個の小さな立方体で大きな立方体を作ると，縦・横・上下に３個ずつ並びます。

　　上から１段ずつ切り分けて考えると，次の図のように赤色の立方体が現れます。

　　　　

　　　４＋１＋４＝９個

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　９個


(2) ６４個の小さな立方体で大きな立方体を作ると，縦・横・上下に４個ずつ並びます。

　　(１)と同様に考えて上から見た図で表すと，次のようになります。

　　　　

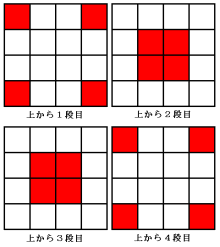
　　　４＋４＋４＋４＝１６個

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１６個


(3) 前の２つの設問の図から考えると，赤色の正方形の位置は上から１段ごとに内側に入
　　っていき，真ん中にきた後それまでと逆に外側に出て行くことがわかります。

　　１７＝４＋４＋１＋４＋４　なので，縦・横・上下に５個ずつ並んでいます。

　　小さい立方体の総数は，

　　　５×５×５＝１２５個

　　白色の立方体の個数は，

　　　１２５−１７＝１０８個

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１０８個

(4) (３)と同様に考えます。

　　２４＝４＋４＋４＋４＋４＋４　なので，縦・横・上下に６個ずつ並んでいます。

　　白色の立方体の個数は，

　　　６×６×６−２４＝１９２個

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１９２個