<問題>
2種類の円柱A,Bがあり,円柱Aは底面の半径が20cm,高さが1cmで,円柱Bは底
面の半径が10cm,高さが2cmです。次の約束に従って,この2種類の円柱を積み上げて
立体を作ります。
(約束1)円柱は底面どうしを重ねて,立体が倒れないように積み上げます。
(約束2)同じ種類の円柱を重ねるときは,互いの底面がずれないように積みます。
(約束3)違う種類の円柱を重ねるときは,円柱Bが円柱Aからはみ出さないように積み
ます。
このとき。次の問いに答えなさい。
(1)
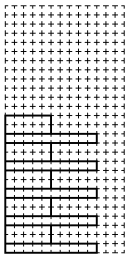
次の図は円柱Aを5個、円柱Bを4個使って作った立体を真横から見たものです。こ
の立体の体積と表面積をそれぞれ求めなさい。ただし,方眼紙の1目盛りは横が4cm,
縦が1cmを表しているものとします。

(2)
円柱Aを5個,円柱Bを4個使って,表面積が最も小さい立体を作りました。この立
体の表面積を求めなさい。
(3)
円柱Aも円柱Bも必ず1個は使って,体積が9420cm3の立体を作ります。表面積が最
も大きくなるように作るとき,A,Bはそれぞれ何個使いますか。また,そのときの表
面積を求めなさい。さらに,このような立体の真横から見た図を1つ,次の方眼紙にか
きなさい。ただし,方眼紙の1目盛りは横が4cm,縦が1cmを表しているものとします。

<解答>
どのように重ねても側面の面積は同じです。底面が他の円柱と重なることで隠されてし
まうことがポイントです。
予め必要な面積や体積を求めておきましょう。
円柱Aの側面積=20×2×3.14×1=125.6cm2
円柱Bの側面積=10×2×3.14×2=125.6cm2
円柱A,Bの側面積は等しいことがわかります。
また、
円柱Aの底面積=20×20×3.14=1256cm2
円柱Bの底面積=10×10×3.14=314cm2
A、B2つの円柱を重ねても隠れない部分の面積=1256−314=942cm2
さらに、
円柱Aの体積=1256×1=1256cm3
円柱Bの体積=314×2=628cm3
(1)
体積はかんたんに求めることができます。
円柱Aの体積×5+円柱Bの体積×4
=1256×5+628×4
=6280+2512
=8792cm3
次に表面積を求めます。

側面の面積の合計
=円柱Aの側面積×5+円柱Bの側面積×4
=125.6×9
=1130.4cm2
図からA、Bが接しているところ(赤線)が6カ所あるので、
底面の面積の合計
=1256×2+942×6
=2512+5652
=8164cm2
これらから表面積は、
1130.4+8164=9294.4cm2
答 体積:8792cm3 表面積:9294.4cm2
(2)
同じ種類の円柱が接している場合が多いほど、表面積は小さくなります。
円柱Aを5個重ねた円柱と円柱Bを4個重ねた円柱で考えると、

側面の面積の合計=125.6×9
=1130.4cm2
A、Bが接しているところが1カ所あるので、
底面の面積の合計
=1256+314+942
=2512cm2
これらから表面積は、
1130.4+2512=3642.4cm2
答 3642.4cm2
(3)
2種類の円柱で体積が9420cm2を作ることができるときを考えます。
9420÷1256=7あまり628 なので、
A7個とB1個、A6個とB3個、A5個とB5個、A4個とB7個、
A3個とB9個、A2個とB11個、A1個とB13個
が考えられます。
次の2つの事がらを考えながら、それぞれの組で表面積が最大になるもの考えます。
側面積の和は円柱の合計数に比例して大きくなる
底面積の和は同じ種類の円柱が接する所が少ないほど大きくなる
○A7個とB1個の場合
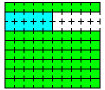
側面積の和=125.6×8=1004.8cm2
底面積の和=1256×2+942×2=4396cm2
表面積=1004.8+4396=5400.8cm2
○A6個とB3個の場合
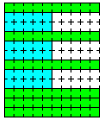
側面積の和=125.6×9=1130.4cm2
底面積の和=1256×2+942×6=8164cm2
表面積=1130.4+8164=9294.4cm2
○A5個とB5個の場合

側面積の和=125.6×10=1256cm2
底面積の和=1256+314+942×9=10048cm2
表面積=1256+10048=11304cm2
○A4個とB7個

側面積の和=125.6×11=1381.6cm2
底面積の和=314×2+942×8=8212cm2
表面積=1318.6+8212=9593.6cm2
これ以降は底面積の和の減り方が側面積の和の増え方より大きくなるので、表面積が
どんどん小さくなります。
答 A5個とB5個、表面積:11304cm2、図は下