＜問題＞

　下の図のように，直線上に長方形と平行四辺形があります。いま，直線上を長方形が毎
秒２cm，平行四辺形が毎秒１cmの速さで矢印の方向へ同時に動き始めます。次の問いに答
えなさい。

　　　　

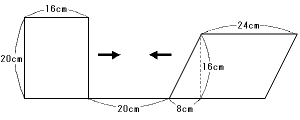
(1) ２つの図形が動き始めてから８秒後に出来る重なった部分の面積を求めなさい。


(2) 重なった部分が正方形になるのは，２つの図形が動き始めてから何秒後ですか。















＜解答＞

２つのものが同時に動く場合には一方を固定して考える必要があります。平行四辺形を動
かさないとすると，長方形は右向きに毎秒３cmの速さで動くことになります。

(1) ８秒後は次図のようになります。

　　　　

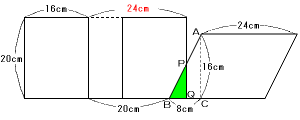
　　三角形ＰＢＱは三角形ＡＢＣと相似です。

　　相似比を求めてＰＱの長さを出します。

    長方形が進んだ距離は，

　　　３×８＝２４cm

　　ＢＱ＝２４−２０＝４cm　だから，

　　　ＢＱ：ＢＣ＝４：８＝１：２

　　ＰＱ：ＡＣも１：２なので，

　　　ＰＱ＝ＡＣ×
　　　　　＝１６cm×
　　　　　＝８cm

　　三角形ＰＢＱの面積は，

　　　ＢＱ×ＰＱ×
　　　　　＝４×８×
　　　　　＝１６ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１６ｃm2


(2) 正方形になるのは次図のようになったときです。

　　　　

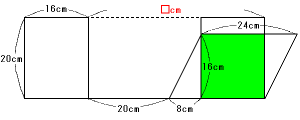
　　図の□の値を求めることが必要です。

　　　□＝２０＋８＋１６＝４４cm

　　毎秒３cmで動いたので，

　　　３４÷３＝１４秒

　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１４秒後