＜問題＞

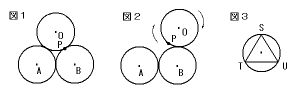
　たがいに接している半径８cmの円Ａ，円Ｂがあります。はじめに図１のように半径８cm
の円Ｏが円Ａと円Ｂの両方に接していて，円Ｏの周上の点Ｐが円Ｂの周上にありました。
円Ｏが図２のように，すべることなく矢印の方向に回転しながら円Ｂ，円Ａの周上を移動
するとき，次の各問いに答えなさい。

　　

[1] はじめて角ＡＢＯの大きさが１２０°になったとき，角ＰＯＢの大きさを求めなさい。

[2] 点Ｐが次に円Ａまたは円Ｂの周上にきたとき，角ＰＯＢの大きさを求めなさい。

[3] 点Ｐがふたたび図１の位置にくるまで円Ｏを移動させたとき，次の(１)，(２)に答え
　　なさい。

　　(1) 点Ｐが円Ａまたは円Ｂの周上にくるのは，図１の点Ｐの位置を含めて何か所あり
　　　　ますか。

　　(2) (１)で求めたすべての点Ｐの位置を頂点とする多角形を作ります。その多角形の
　　　　面積は，図３の半径８cmの円周上の３点Ｓ，Ｔ，Ｕを結んでできる正三角形の面
　　　　積の何倍ですか。















＜解答＞

[1] ３つの円は同じ半径なので，円Ｏが転がる時に動いた部分の弧の長さは等しく，また
　　中心角も等しくなります。

　　はじめの三角形角ＡＢＯは正三角形なので，もともと角ＡＢＯは６０度です。それが
　　１２０度になるので，

　　　１２０−６０＝６０度

　　点Ｐも円周上で接点の位置から６０度進んでいます。

　　　　

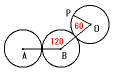
　　よって角ＰＯＢ＝６０度です。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　６０度


[2] 円Ｂでは円周の３分の２，２４０度分回転したきは次の図のようになります。

　　　　

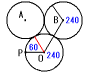
　　点Ｐが再び接点になるにはあと６０度回転する必要があります。

　　　　

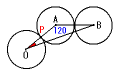
　　上の図で三角形ＡＯＰはＯＢを底辺とする二等辺三角形で，角ＰＯＢはその底角にあ
　　たります。

　　頂角ＯＡＢは１２０度なので，

　　　角ＰＯＢ＝（１８０−１２０）÷２＝３０度

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３０度


[3] (1) ２つの円Ａ，Ｂに同時に接した瞬間に６０度進んだことになります。したがって
　　　　３００度進むと点Ｐが接点になります。

　　　　

　　　　円Ｏが接する部分は上の図の緑のおうぎ形の弧の部分です。順に点を打っていく
　　　　と，次の図のようになります。元の位置で接する最後の回転では同時に接すると
　　　　きが２度あります。そのため２４０度だけ進んでいます。

　　　　

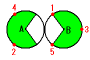
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　５か所

　　(2) 与えられた正三角形を次のように３つの二等辺三角形に分けます。

　　　　

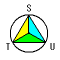
　　　　できた五角形を次のように１１個の正三角形と二等辺三角形に分けると，それぞ
　　　　れが上の図の二等辺三角形１つと等しい面積になります。

　　　　

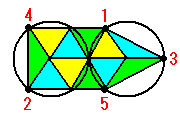
　　　　　１１÷３＝３

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　３倍