＜問題＞

　長さ３cmの棒が何本かあります。これらの棒を使って，正三角形や正方形を作ります。
棒を折ったり曲げたり一部分を使ったりすることはできません。また，どの図形もくっつ
いたり，重なったりしません。
　たとえば，６本の棒で正三角形を作るとすると，一辺の長さが６cmの正三角形を１個作
る作り方と，一辺の長さが３cmの正三角形を２個作る作り方の２通りあります。

　次の問いに答えなさい。

(1) １２本の棒を全部使って正三角形だけを作る作り方は何通りありますか。


(2) １９本の棒を全部使って正三角形と正方形を作る作り方は何通りありますか。















＜解答＞

(1) １辺に使う本数の３倍の本数が正三角形を１個作るのに必要です。よって正三角形を
　　１個作るには必ず「３の倍数」本の棒を使うことがわかります。

　　　

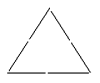
　　上の図では，１辺の棒の数が２本なので，２×３＝６本使っています。　

　　そこで，１２をいくつかの３の倍数の和に直して数えることにします。

　　１２以下の３の倍数は３，６，９，１２なので，大きい方から決めていくと，

　　　　１２＝１２
　　　　１２＝９＋３
　　　　１２＝６＋６
　　　　１２＝６＋３＋３
　　　　１２＝３＋３＋３＋３

　　よって，５通りです。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　５通り


(2) 正三角形と同様に考えると，正方形を１個作るのに必要な棒は「４の倍数」本です。

　　よって，１９をいくつかの３または４の倍数の和に直して数えることにします。

　　１９以下の３または４の倍数は３，４，６，８，９，１２，１５，１６，１８なので
　　大きい方から決めていくと，

　　　　１９＝１６＋３
　　　　１９＝１５＋４
　　　　１９＝１２（＊）＋４＋３
　　　　１９＝９＋６＋４
　　　　１９＝９＋４＋３＋３
　　　　１９＝８＋８＋３
　　　　１９＝８＋４＋４＋３
　　　　１９＝６＋６＋４＋３
　　　　１９＝６＋４＋３＋３＋３
　　　　１９＝４＋４＋４＋４＋３
　　　　１９＝４＋３＋３＋３＋３＋３

　　以上のように１１通りできますが，このうちで＊をつけた１２は正三角形と正方形ど
　　ちらでもできる数なので，１９＝１２（＊）＋４＋３は２通りあると考える必要があ
　　ります。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１２通り