＜問題＞

　図１のような長方形の紙があります。次の問いに答えなさい。

　

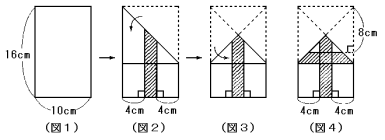
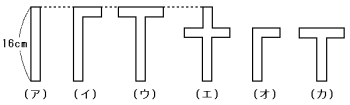
(1) 図２のように折り，斜線の部分を切り取って広げたときの図を(ア)から(カ)の中から
　　選び，そのまわりの長さも求めなさい。


(2) 図３のように折り，斜線の部分を切り取って広げたときの図を(ア)から(カ)の中から
　　選びなさい。


(3) 図４の斜線の部分を切り取って広げたときの面積を求めなさい。

　















＜解答＞

(1) 切り取られた部分は開くと折り目について線対称になります。

　　次の図で緑の部分と青い部分が線対称です。

　　

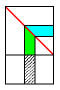
　　よってできた図形は（オ）です。

　　周りの長さは，縦１２cm横６cmの長方形と同じなので，

　　　　（１２＋６）×２＝３６cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答（オ），３６cm


(2) ２度折ってから切り取っているので線対称の図形を２度考えます。

　　次の２つの図で緑の部分と青い部分が線対称です。

　

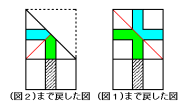
　　よってできた図形は（エ）です。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答（エ）


(3) 同様に考えるとできた図形は次の図の赤い部分だとわかります。

　　

　　元の長方形全体から１辺２cmの正方形４つ，縦６cm横４cmの長方形２つを除いた図形
　　なので，

　　　１６×１０−（２×２×４＋６×４×２）＝９６ｃm2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　９６ｃm2