＜問題＞

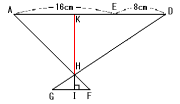
　＜図１＞の長方形ＡＢＣＤにおいて，ＡＥ＝１６cm，ＥＤ＝８cm，ＡＢ＝１２cm，ＣＦ
　＝１２cmです。

　

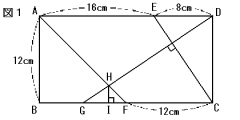
　＜図２＞，＜図３＞は，＜図１＞の長方形から一部を抜き出したものです。

　　　　

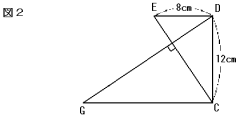
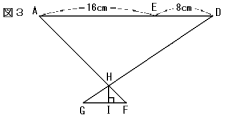
　これらを利用して，つぎの問いに答えなさい。

(1) ＣＧの長さを求めなさい。


(2) ＨＩの長さを求めなさい。


(3) ＢＩの長さを求めなさい。















＜解答＞

相似な三角形の組を見つけて考えることが大切です。

(1) 図の赤い三角形ＪＣＤは三角形ＤＣＥと相似で、三角形ＣＧＤとも相似です。
　　
　　

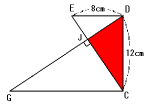
　　よって三角形ＤＣＥと三角形ＣＧＤが相似になるので、

　　　ＤＣ：ＤＥ＝ＣＧ：ＣＤ＝１２cm：８cm＝３：２

　　これから、

　　　ＣＧ＝ＣＤ×＝１２cm×＝１８cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１８cm


(2) 三角形ＡＤＨと三角形ＦＧＨが相似で、その相似比を求めると、

　　　ＡＤ：ＦＧ＝（１６cm＋８cm）：（１８cm−１２cm）＝４：１

　　２つの三角形の高さの比ＫＩ：ＨＩも４：１です。

　　

　　これから、

　　　ＨＩ＝１２cm×＝２．４cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　２．４cm


(3) 三角形ＡＢＦと三角形ＨＩＦは相似です。

　　

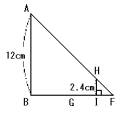
　　また、ＢＦ＝１６cm＋８cm−１２cm＝１２cmなので、ＡＢ＝ＢＦとなり、

　　三角形ＡＢＦと三角形ＨＩＦはともに直角二等辺三角形だとわかります。

　　よって、

　　　ＩＦ＝ＨＩ＝２．４cm

　　　ＢＩ＝ＢＦ−ＩＦ＝１２cm−２．４cm＝９．６cm

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　９．６cm