<問題> 次の図1で,点Pは点Aを出発し,毎秒1cmの速さで「A→B→C→F→E→D→C→ F→A」の順に動きます。点Qは,点Pが出発してから16秒後に毎秒2cmの速さで点P と同じ順に動きます。次の問いに答えなさい。
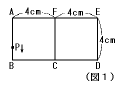
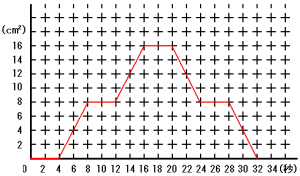
(1) 3つの点A,B,Pを頂点とする三角形において,点Pが出発してからの時間と三角
形の面積の関係をグラフに表しなさい。

(2) 3つの点A,B,Qを頂点とする三角形において,点Pが出発してからの時間と三角
形の面積の関係をグラフに表しなさい。

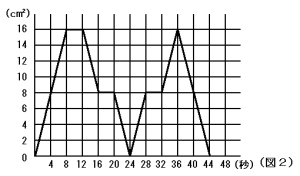
(3) 点Rが点Aを出発して毎秒1cmの速さで動くとき,3つの点A,B,Rを頂点とする
三角形の面積が図2のように変化しました。点Rの動く順序を「 」の例にならって答
えなさい。
<解答>
(1) 点Pがどの辺上にあるかによって高さが変わるので時間と面積の関係が異なります。
0〜 4秒後 辺AB上で,三角形はできない
4〜 8秒後 辺BC上で,高さはBPで次第に増える
8秒後の面積は, 4×4÷2=8cm2
8〜12秒後 辺CF上で,高さはBCで一定
12秒後の面積は, 4×4÷2=8cm2
12〜16秒後 辺FE上で,高さはAPで次第に増える
16秒後の面積は, 4×8÷2=16cm2
16〜20秒後 辺ED上で,高さはAEで一定
20秒後の面積は, 4×8÷2=16cm2
20〜24秒後 辺DC上で,高さはBPで次第に減る
24秒後の面積は, 4×4÷2=8cm2
24〜28秒後 辺CF上で,高さはBCは一定
28秒後の面積は, 4×4÷2=8cm2
28〜32秒後 辺FA上で,高さはAPで次第に減る
32秒後の面積は 0
境となる時点の面積を計算して直線で結ぶとグラフが完成します。
答
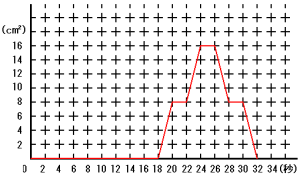
(2) 上と同様に点Qの位置による高さの変化を考えます。
0〜16秒後 まだ頂点Aにあるので,三角形はできない
16〜18秒後 辺AB上で,三角形はできない
18〜20秒後 辺BC上で,高さはBPで次第に増える
20秒後の面積は, 4×4÷2=8cm2
20〜22秒後 辺CF上で,高さはBCで一定
22秒後の面積は, 4×4÷2=8cm2
22〜24秒後 辺FE上で,高さはAPで次第に増える
24秒後の面積は, 4×8÷2=16cm2
24〜26秒後 辺ED上で,高さはAEで一定
26秒後の面積は, 4×8÷2=16cm2
26〜28秒後 辺DC上で,高さはBPで次第に減る
28秒後の面積は, 4×4÷2=8cm2
28〜30秒後 辺CF上で,高さはBCは一定
30秒後の面積は, 4×4÷2=8cm2
30〜32秒後 辺FA上で,高さはAPで次第に減る
32秒後の面積は 0
境となる時点の面積を計算して直線で結ぶとグラフが完成します。
答
(3) 底辺がABで一定なので,点Rの位置による高さの変化を考えて求めます。
面積が 8cm2の場合,高さは 8×2÷4=4cm なので,辺CF上
面積が16cm2の場合,高さは 16×2÷4=8cm なので,辺DE上
0〜 8秒後 高さは一定の割合で増加して8cmになる
よって,A→F→E
8〜12秒後 高さは8cmで一定
よって,E→D
12〜16秒後 高さは一定の割合で減少して4cmになる
よって,D→C
16〜20秒後 高さは4cmで一定
よって,C→F
20〜24秒後 高さは一定の割合で減少して0になる
よって,F→A
24〜28秒後 高さは一定の割合で増加して4cmになる
よって,A→F
28〜32秒後 高さは4cmで一定
よって,F→C
32〜36秒後 高さは一定の割合で増加して8cmになる
よって,C→D
36〜44秒後 高さは一定の割合で減少して0になる
よって D→C→B
これらをまとめると,
A→F→E→D→C→F→A→F→C→D→C→B
答
A→F→E→D→C→F→A→F→C→D→C→B