算数

　　　　「円が転がる時に通った跡」

　　　　転がる円の通った跡の面積に関する問題はよく出されます。以前は多角形の周囲を完全に
　　　　１周するものも多く出されましたが，最近は以下のような問題が増えています。このよう
　　　　な問題では，面積を求める部分をいくつか計算がやりやすい形に分けることが必要です。

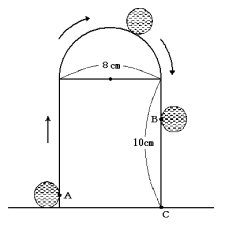
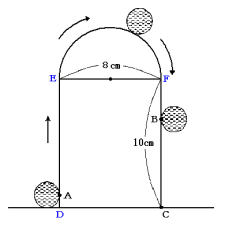
＜問題＞ 　半径１cmの円を図のように矢印の方向にすべることなく４回転させたら，Ａ地点からＢ地点に移動しまし 　た。次の問いに答えなさい。 　　 (1) ＢＣ間の長さを求めなさい。 (2) Ａ地点からＢ地点まで移動する間に，この円が通った部分の面積を求めなさい。 ＜解答＞ (1) ＢＣの長さは，長方形の縦２倍と弧ＥＦの長さの和と線分ＡＤと曲線ＡＢの長さ（半径１cmの円の４周 　　分）の和の差です。 　　 　　長方形の縦２倍と弧ＥＦの長さの和は， 　　　１０×２＋８×３．１４× 　　　＝３２．５６cm 　　線分ＡＤと曲線ＡＢの長さの和は， 　　　１＋１×２×３．１４×４＝２６．１２cm 　　よって， 　　　３２．５６−２６．１２＝６．４４cm 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　答　６．４４cm (2) 円が通った跡は次の図の赤・青・緑の部分を合わせた部分です。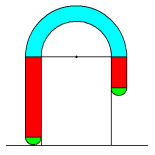 　　 　　赤の部分は，ともに横２cmの長方形で，縦の長さが， 　　　長い方　１０−１＝９cm 　　　短い方　１０−６．４４＝３．５６cm 　　面積の和は， 　　　（９＋３．５６）×２＝２５．１２ｃm2 　　青の部分は，直径１２cmの半円から直径８cmの半円を除いた部分なので， 　　　６×６×３．１４×−４×４×３．１４× 　　　＝３１．４ｃm2 　　緑の部分は，合わせると半径１cmの円になるので， 　　　１×１×３．１４＝３．１４ｃm2 　　よって， 　　　２５．１２＋３１．４＋３．１４＝５９．６６ｃm2 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　５９．６６cm2

ページTopへ