円柱の形をした容器A、B、Cがあります。Aは底面積60cm2で深さ30cm、Bは底面積
24cm2で深さ15cm、Cは深さ30cmです。最初Aの容器には深さ12cmまで水が入っていまし
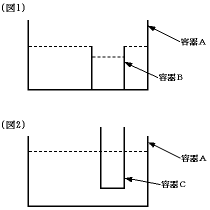
たが、そこに空のBの容器を(図1)のようにAの底につくまで沈めていくと、水の一部が
あふれてBの容器に入ってしまいました。
(1) Bの答器に入っている水の深さは何cmですか。
(2) Bの容器に入っていいた水をCの容器に移して、Bの容器をAの容器に沈めていくと
底面がAの容器の底から2cmのところで(図2)のようにAとCの水面が同じ高さになり
ました。Cの容器の底面積は何cm2ですか。また、そう答えた理由も書きなさい。
<解答>
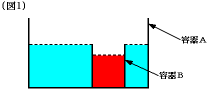
(1) 容器Bに入っている水(図の赤い部分)の体積と容器Aで容器Bをのぞいた部分に入
っている水(図の青い部分)の体積の和は、最初から容器Aに入っていた水の体積と
と同じです。
最初から容器Aに入っていた水の体積は、
60cm2×12cm=720cm3
容器Aで容器Bをのぞいた部分に入っている水の体積を求めると、
底面積=60cm2−24cm2=36cm2
深さ=15cm
体積=36cm2×15cm=540cm3
これから、容器Bに入っている水の体積は、
720cm3−540cm3=180cm3
その深さは、
180cm3÷24cm2=7.5cm
答 7.5cm
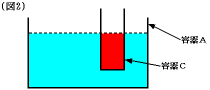
(2) 容器Cに入っている水(図の赤い部分)の体積と容器Aで容器Cをのぞいた部分に入
っている水(図の青い部分)の体積の和は、最初から容器Aに入っていた水の体積と
と同じです。また、水面が同じ高さなので水の深さは元と同じ12cmです。
容器Cに入っている水は、
体積=180cm3
深さ=12cm−2cm=10cm
よって、
底面積=180cm3÷10cm=18cm2
答 18cm2