算数

　　　　「立体図形の底面積と高さ」

　　　　比例・反比例の考え方を使って解く図形問題はほとんどが「線分比と面積比」に関するも
　　　　のです。が，この問題のように「底面積比と体積比」に関する問題も出されることがあり
　　　　ます。底面積を割合で表して計算します。

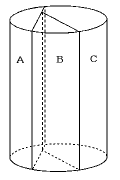
＜問題＞ 図のような円柱の容器があります。この容器の底面に垂直に２枚のしきりを入れて，Ａ，Ｂ，Ｃの３つの部分に分けました。このＡ，Ｂ，Ｃの部分に同じ量の水を入れたところ，水面の高さがそれぞれ９cm，７cm，３cmになりました。ただし，しきりの厚さは考えません。 次の各問いに答えなさい。 　　　 (1) Ａ，Ｂ，Ｃの底面積の比を最も簡単な整数で表しなさい。 (2) この２枚のしきりをとると，水面の高さは何cmになりますか。 ＜解答＞ (1) 角柱・円柱などの柱体では，体積が等しいときに底面積と高さとは反比例します。 　　高さの比　　Ａ：Ｂ：Ｃ＝９：７：３ 　　底面積の比　Ａ：Ｂ：Ｃ＝：：＝７：９：２１ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　７：９：２１ (2) Ａ，Ｂ，Ｃの底面積をそれぞれ７，９，２１として，水の体積を求めると， 　　　７×９＋９×７＋２１×３＝１８９ 　　円柱の容器全体の底面積は， 　　　７＋９＋２１＝３７ 　　よって，しきりを取り除いたときの深さは， 　　　１８９÷３７＝５cm 　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　５cm

ページTopへ