<問題>
次の図で,AP:PB=AQ:QC=1:2で,ACとRBは平行です。また,三角形ABCの面積は9cm2です。
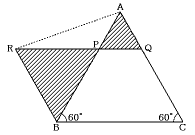
次の問いに答えなさい。
(1) 三角形APQの面積は何cm2ですか。
(2) 斜線部分の面積は何cm2ですか。
(3) 四角形ARBCの面積と,(2) で求めた面積との比を,もっとも簡単な整数の比で
表しなさい。
<解答>
(1) AP:PB=AQ:QC=1:2なので、PQとBCは平行です。
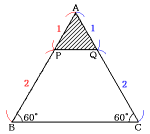
よって対応する2つの角の大きさが等しいので、三角形ABCと三角形APQは相似
です。
相似比はAB:APから求めると、
(1+2):1=3:1
面積比は、
(3×3):(1×1)=9:1
これから、三角形APQの面積は三角形ABCの面積の
9cm2×
答 1cm2
(2) 斜線部分の面積は、2つの三角形APQ、BPRの面積の和です。
ACとRBが平行なので、この2つ三角形も相似です。
相似比は1:2で、面積比は1:4です。
三角形APQの面積は1cm2なので、三角形BPRの面積は、
1cm2×4=4cm2
斜線部分の面積は、
1cm2+4cm2=5cm2
答 5cm2
(3) 四角形ARBCの面積は、3つの三角形ABC、BPR、APRの面積の和です。
このうちで面積がわかっていないのは三角形APRです。
三角形APRは三角形APQと高さが等しいので、
この2つの三角形の面積比は底辺の長さの比になります。
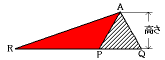
(2)で用いた相似から、PR:PQ=PB:PA=2:1です。
三角形APRの面積は三角形APQの面積の2倍なので、
1cm2×2=2cm2
四角形ARBCの面積は、
9cm2+4cm2+2cm2=15cm2
求める比は、
15cm2:5cm2=3:1
答 3:1