<問題>
下の図1のような容器にA,Bの2つの蛇口から毎分一定量の水を入れます。Aの蛇口で水を15分間入れ、その後、2つの蛇口A,Bで満水になるまで水を入れました。図2は、そのときの時間と水面の高さの関係を表したものです。
次の問いに答えなさい。
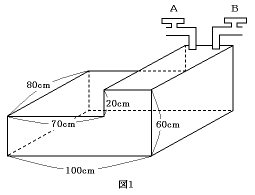
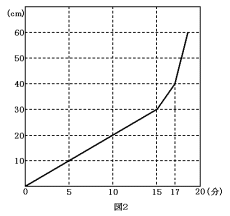
(1) Aの蛇口から出る水の量は毎分何リットルですか。
(2) Bの蛇口から出る水の量は毎分何リットルですか。
(3) 容器が満水になるのは、水を入れ始めてから何分何秒後ですか。
<解答>
(1) 始めから15分間に容器にたまった水の量(次図の青い部分)を求めます。
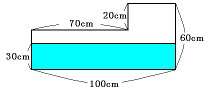
この量は合計で、
80×100×30=240000cm2=240リットル
これから、Aの蛇口から出る水の量は、
240÷15=毎分16リットル
答 毎分16リットル
(2) 15分後から17分後までの2分間に容器にたまった水の量(次図の青い部分)を求 めます。
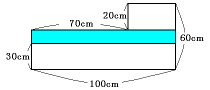
この量は合計で、
80×100×(40−30)=80000cm2=80リットル
これから、A・B2つの蛇口から出る水の量は、
80÷(17−15)=毎分40リットル
Bの蛇口から出る水の量は、
40−16=毎分24リットル
答 毎分24リットル
(3) 17分後から後で容器にたまる水の量(次図の青い部分)を求めます。
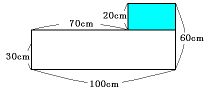
この量は合計で、
80×(100−70)×20=48000cm2=48リットル
この水の量がたまる時間は、
48÷40=1.2分=1分12秒
容器が満水になるのは、
17分+1分12秒=18分12秒
答 18分12秒後