<問題>
1辺が2cmの立方体があります。その立方体24個を積み重ねて、[図1]のような立体を作りました。
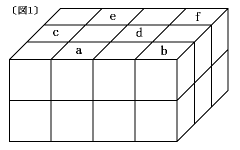
(1) この立体の表面積は何cm2ですか。
(2) [図1]の立体からaの立方体を取ったら[図2]のようになりました。[図2]
の立体は[図1]の立体と比べて、表面積は何cm2増加しましたか。
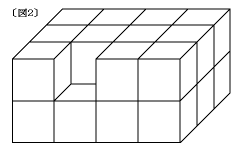
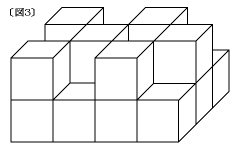
(3) [図1]の立体からa,b,c,d,e,fの6つの立方体を取ったら[図3]のよ
うになりました。[図3]の立体は[図1]の立体と比べて、表面積は何cm2増加し
ましたか。考えた過程も書きなさい。
<解答>
(1) 立方体や直方体を組み合わせて作った立体は、前後、左右、上下の6つの方向か
ら見た形をもとにして考えます。
前後からは、正方形8個ずつ
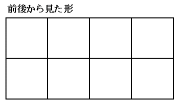
左右からは、正方形6個ずつ
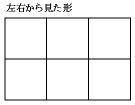
上下からは、正方形12個ずつ
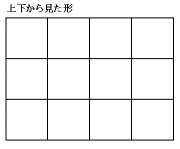
それぞれ見えます。
立方体の6面を作っている正方形の面積は、
2×2=4cm2
この立体の表面積は、
4cm2×(8個×2+6個×2+12個×2)=208cm2
答 208cm2
(2) (1) と同様に6方向から見た形をもとに考えます。
前後からは、正方形8個ずつ
左右からは、正方形6個ずつ
上下からは、正方形12個ずつ
それぞれ見えます。
しかし、次の図の赤い面2つが隠れてどの方向からも見えません。
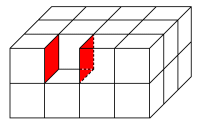
したがって、表面積はこの2面の分だけ増加します。
4cm2×2=8cm2
答 8cm2
(3) これも(1) と同様に6方向から見た形をもとに考えます。
前後からは、正方形8個ずつ
左右からは、正方形6個ずつ
上下からは、正方形12個ずつ
それぞれ見えます。
しかし、次の図の赤・青・緑の合わせて10面が隠れてどの方向からも見えません。
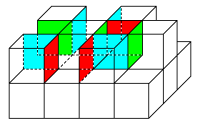
したがって、表面積はこの10面の分だけ増加します。
4cm2×10=40cm2
答 40cm2