<問題>
図のような,各辺の長さが8cmの正四角すいの枠があります。F,Iは辺AB,AEのま
ん中の点で,辺AGと辺GCの長さの比は3:1で,辺AHと辺HDの長さの比も3:1
です。四角形FGHIの部分には紙がはってあります。 この正四角すいを机の上において,真上から平行な光を当てたとき,四角形FGHIの影ができました。
このとき,次の問いに答えなさい。
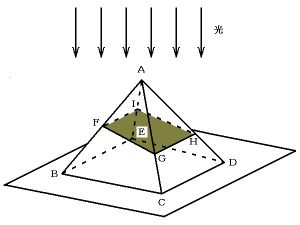
(1) 四角形FGHIの影は机にどのようにうつりますか。
解答欄に斜線で書き込みなさい。
(2) 机にうつった四角形FGHIの影の面積を求めなさい。
<解答>
(1) 台形FGHIの真下にあたる部分が影になります。
考えやすくするために,4頂点F,G,H,Iの真下の点を結んで考えます。
次のように,3点A,B,Dを通る平面を考えると,2頂点F,Hの真下の点
F’,H’は次の図のような位置になります。
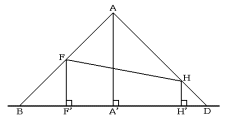
AA’,FF’,HH’の線分は互いに平行なので,
BF’:F’A’=BF:FA=1:1
DH’:H’A’=DH:HA=1:3
この関係を利用して,2点F’,H’の位置を決めます。
同様にして残る2頂点G,Iの真下の点G’,I’を求めて結ぶと,
以下のようになります。
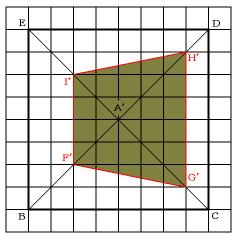
答は,上の影の部分です。
(2) (1)の結果から,影は台形になることがわかります。
この台形は上底が4cm,下底が6cm,高さが5cmなので,
(4+6)×5÷2=25cm2
答 25cm2