＜問題＞
１辺の長さが１ｃｍの正方形ＡＢＣＤを下の図のように分けます。
Ｅ、Ｆは辺ＡＤ、辺ＢＣをそれぞれ１：２に分ける点、Ｇ、Ｈは辺ＦＥ、辺ＣＤをそれぞ
れ１：２に分ける点、Ｉ、Ｊは辺ＥＤ、辺ＧＨをそれぞれ１：２に分ける点です。
このとき次の問に答えなさい。
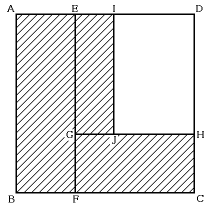
(1) 斜線部分の面積を求めなさい。
(2)
＋
＋
＋
＋
＋
＋
＋
を計算しなさい。＜解答＞
(1) 長方形ＩＪＨＤの面積を求めて、正方形ＡＢＣＤの面積から引いて考えます。
辺ＩＪの長さは、辺ＡＢの長さの（１−
）倍なので、１ｃｍ×（１−
）＝
ｃｍ辺ＥＤの長さは、辺ＡＤの長さの（１−
倍）になり、辺ＩＤの長さは、辺ＥＤの長さの（１−
倍）なので、１ｃｍ×（１−
）×（１−）＝
ｃｍ長方形ＩＪＨＤの面積は、
ｃｍ×ｃｍ＝
ｃm2よって、斜線部の面積は、
１ｃm2−
ｃm2＝
ｃm2答
ｃm2(2)
＋＋＋＋＋＋＋ の計算は上の面積計算を式化したものです。
そこで(1) と同じように正方形全体の面積から白い長方形の面積を引いて求める方法
を利用します。
残りの部分をいつも１：２に分けていくので、白い長方形の面積は最後に加えた長方
形の２倍の面積になります。
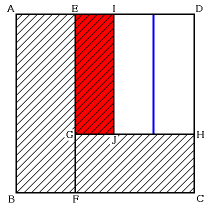
これを利用すると、
＋＋＋＋＋＋＋＝１−
×２＝１−
＝
答